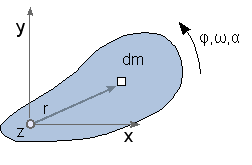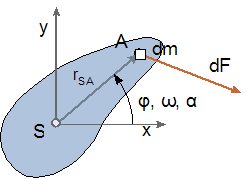
Die kinematische Formulierung der ebenen Bewegung eines Körpers haben wir bereits in der vergangenen Vorlesung gehandelt. Das körperfeste Koordinatensystem soll nun im Massenmittelpunkt liegen. Demnach gelten hier die analogen kinematischen Beziehungen
(c)aA =
aS + α·
r^SA − ω
2·
rSA
Wenn nun auf ein differentielles Masseteilchen dm die differentielle Kraft dF wirkt, so lautet das dynamische Grundgesetz in der Fassung von d'Alembert:
Einsetzen von (c) in (d) führt auf
(e)d
F −
aS·dm − α·
r^SA·dm + ω
2·
rSA·dm =
0
Die Integration ergibt
(f)∫d
F −
aS ∫dm − α ∫
r^SA·dm + ω
2 ∫
rSA·dm =
0
Die statischen Momente bezüglich der Schwerpunktachsen verschwinden bekanntlich, damit sind die Integrale
∫rSA·dm = 0
∫r^SA·dm = 0
Null und es gilt hier ebenfalls der Schwerpunktsatz
Wir multiplizieren nun Gleichung (e) skalar mit r^SA und erhalten
dF·r^SA − aS·r^SAdm − α·r^SA·r^SAdm + ω2·rSA·r^SAdm = 0
Der erste Summand entspricht dem Moment dM der Kraft dF bezüglich des Schwerpunkts.
Der letzte Summand dagegen überlebt diese Operation nicht, da definitionsgemäß rSA und r^SA zwei zueinander orthogonale Vektoren sind. Es verbleibt somit
dM − aS·r^SAdm − α·r2SA dm = 0
Die nun folgende Integration, bei der wiederum die statischen Momente bezüglich der Schwerpunktachsen verschwinden, liefert schliesslich mit Θ = ∫r2 dm den Momentensatz (Drallsatz)
M − Θ·α = 0
den wir bereits bei der Rotation eines Körpers um eine feste Achse gefunden haben.
Es gilt also für die allgemeine ebene Starrkörperbewegung mit dem Schwerpunkt als Bezugspunkt der
Schwerpunkt– und Momentensatz
in Komponentenform
∑ Fx − m·aSx = 0
∑ Fy − m·aSx = 0
∑ M − Θ·α = 0