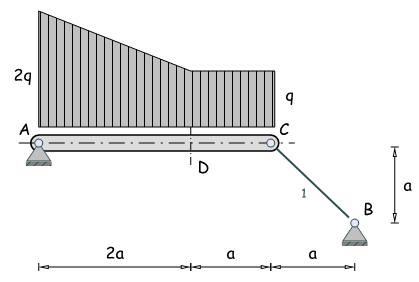
 Ein Balken ist statisch bestimmt mittels Festlager A und Stab 1 gelagert und trägt die skizzierte Streckenlast.
Ein Balken ist statisch bestimmt mittels Festlager A und Stab 1 gelagert und trägt die skizzierte Streckenlast.
- Ermitteln Sie die Schnittgrössen des Balkens an der Stelle D
- Welchen Radius muss der Stab 1 mit Kreisquerschnitt erhalten, wenn eine Knicksicherheit von 2 eingehalten werden muss?
Geg: q = 2 kNm ; a = 1 m; E = 105 Nmm2
Lösung:
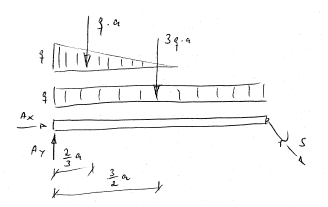
Lager-/Stabkräfte
∑ Fx ≡ Ax + 12√ 2 S = 0
∑ Fy ≡ Ay − 12√ 2 S − qa − 3qa = 0
∑ MA ≡ −12√2 S·3a − 3qa·32a − qa·23a = 0
Ax = 3118 qa = ... = 3.4 kN
Ay = 4118 qa = ... = 4.6 kN
S = −3118 √ 2 qa = ... = −4.9 kN
Schnittgrössen
→ : −N − 12 √ 2 ·3118 √ 2 qa = 0
↑ : Q + 12 √ 2 · 3118 √ 2 qa − qa = 0
↵ : −M + 3118 √ 2 qa · 12 √ 2 a − qa · a2 = 0
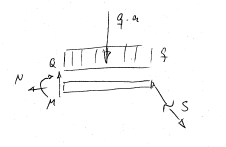
N = −3118 qa = ... = −3.4 kN
Q = 1318 qa = ... = 1.4 kN
M = 119 qa2 = ... = 2.4 kNm
Sicherheit gegen Knicken nach Euler
2 · S = π2 E·Iminlk2
Imin = 14 π r4
lk = √ 2 · a
r = (16 S a2π3 E)1⁄4 = (16·4900·10002π3·105 N·mm2·mm2N)1⁄4 = 70 mm
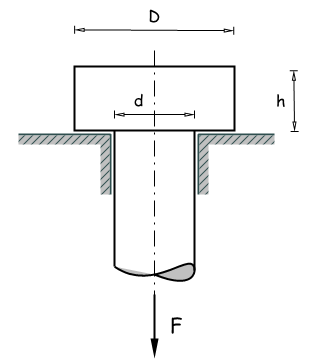 Ein Zugbolzen mit dem Kopfdurchmesser ØD, der Kopfhöhe h und dem Schaftdurchmesser Ød = 10 mm wird durch die Kraft F = 10 kN belastet. Welche Werte sind für D und h zu wählen, wenn die zul. Scherspannung 60 N⁄mm2 und die zul. Flächenpressung 20 N⁄mm2 nicht überschritten werden darf?
Ein Zugbolzen mit dem Kopfdurchmesser ØD, der Kopfhöhe h und dem Schaftdurchmesser Ød = 10 mm wird durch die Kraft F = 10 kN belastet. Welche Werte sind für D und h zu wählen, wenn die zul. Scherspannung 60 N⁄mm2 und die zul. Flächenpressung 20 N⁄mm2 nicht überschritten werden darf? Ein Balken ist statisch bestimmt mittels Festlager A und Stab 1 gelagert und trägt die skizzierte Streckenlast.
Ein Balken ist statisch bestimmt mittels Festlager A und Stab 1 gelagert und trägt die skizzierte Streckenlast.

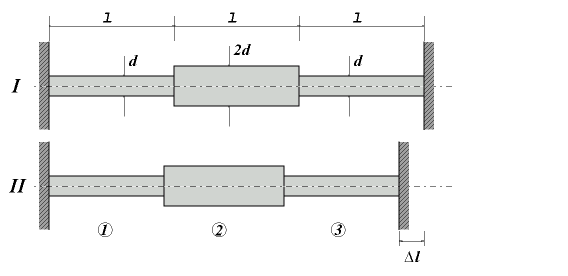
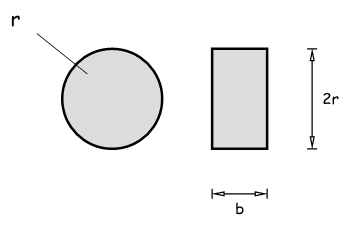 Ein Balken mit Kreisquerschnitt soll durch einen mit Rechteckquerschnitt gleicher Höhe ersetzt werden. Das Widerstandsmoment bezüglich der horizontalen x-Achse soll sich dabei nicht ändern. Ermitteln Sie
Ein Balken mit Kreisquerschnitt soll durch einen mit Rechteckquerschnitt gleicher Höhe ersetzt werden. Das Widerstandsmoment bezüglich der horizontalen x-Achse soll sich dabei nicht ändern. Ermitteln Sie
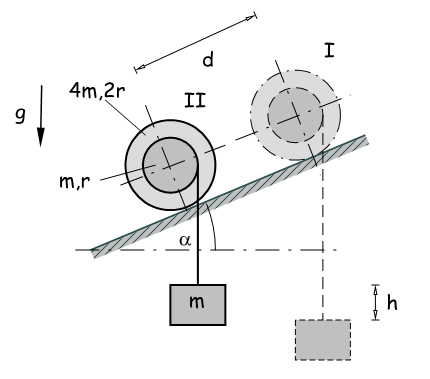 Eine gestufte Zylinderrolle mit dem äusseren Radius 2r und dem inneren Radius r läuft aus der Ruheposition I in 4 Umdrehungen bis zur Position II eine schiefe Ebene herab. Während dieser Bewegung wird eine Masse m über ein Seil aufgewickelt. Ermitteln Sie
Eine gestufte Zylinderrolle mit dem äusseren Radius 2r und dem inneren Radius r läuft aus der Ruheposition I in 4 Umdrehungen bis zur Position II eine schiefe Ebene herab. Während dieser Bewegung wird eine Masse m über ein Seil aufgewickelt. Ermitteln Sie

Bei Aufgabenteil b ist doch sicher klein d im Nenner gemeint oder???? Ja aber ganz sicher!!!!
Ganz sicher!!
Genau und deswegen wird das jetzt geändert! 16.03.06 CSE