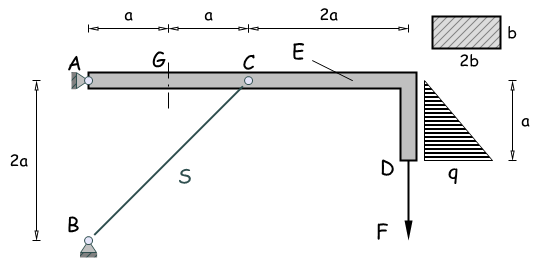
Ein einseitig eingespannter, biegeweicher, dehnstarrer Rahmen wird an seinem Ende durch die skizzierte Einzelkraft F belastet.
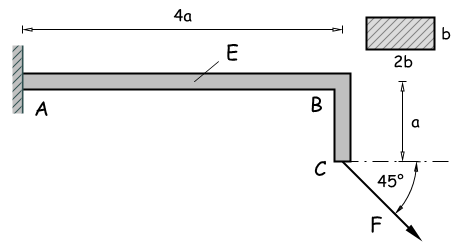
Ermitteln Sie
- die Vertikalverschiebung des Rahmenpunkts B.
- die Horizontalverschiebung des Rahmenpunkts C (vertikalen Rahmenteil bitte als starr annehmen).
Geg: a = 25 cm, b = 25 a, F = 1 kN, E = 2.1·105 Nmm2
—-
Lösung 3a
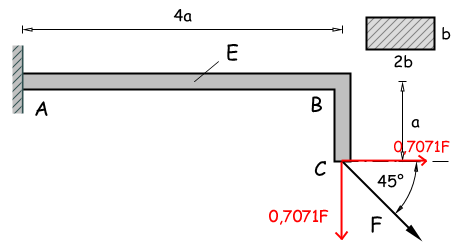
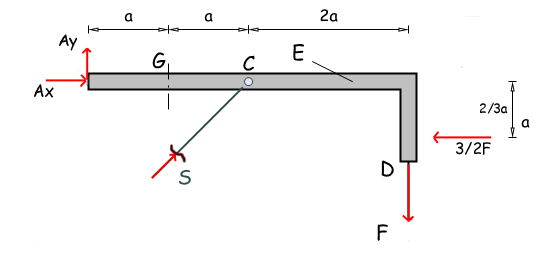
Durch Superposition werden die Lastfälle aufgeteilt und nacher Addiert.
Fall 1
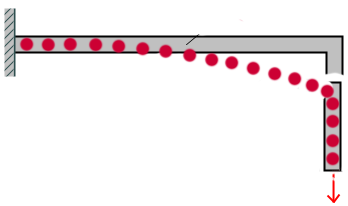
(1)−w
1 =
13·
12·√2·F·l3E·I
mit
(2)I =
112·2b·b
3 =
16·b
4 =
16·
16625·a
4
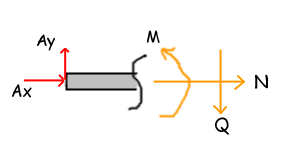
Fall 2
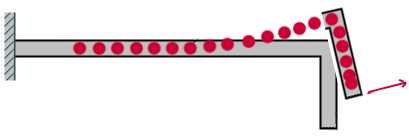
mit
und I wie in Gleichung 2
Durch Addition der beiden Werte erhalten wir die Gesamtverschiebung wges
hier eingesetzt 3 mit 4, 1
(6)w
ges =
12·
12·√2·Fa·(4a)2E·I −
13·
12·√2·F·(4a)3E·I
(7)w
ges = (4 −
323)·
√2·Fa3E·I
I ersetzt durch 2
(8)w
ges =
−2500016·
√2·Fa3E·a4
(9)w
ges =
−31252·
√2·10002,1·105·250
Der Balken senkt sich somit im Punkt B um -0,0420 mm.
Lösung 3b
Wie oben kann nun mit der Verschiebung in der Horizontalen verfahren werden.
Der Winkel α der sich als Tangente zum endpunkt des Balkens ergibt ist gleich dem Winkel der sich zwischen Vertikalem Balkenstüch und Normalen einstellt. Die Verschibung in x ist somit Δxi = sinα·a.
(1)− Δx
1=sin·
arctan12·
F·l2E·I·a
(2)Δx
2=sin·arctan
M·lE·I·a
(3)I =
16·b
4 =
16·(
25·a)
4
Δxges = (2) + (1) mit (3) Eingesetzt
(5)Δx
ges = sin·arctan
M·lE·I·a + (− sin·arctan
12·
F·l2E·I·a)
(6)(sin arctan
18754·
√2·10002,1·105·250)·(−1)
Der Punkt C verschiebt sich in der Horizontalen um -0,01265 mm
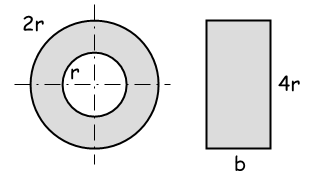 Ein Balken mit Rohrquerschnitt soll durch einen Balken mit Rechteckquerschnitt unter Beibehaltung des Widerstandsmoments Wx ersetzt werden.
Ein Balken mit Rohrquerschnitt soll durch einen Balken mit Rechteckquerschnitt unter Beibehaltung des Widerstandsmoments Wx ersetzt werden.