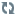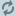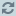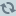In Mechanics and Vector Graphics we inevitably need vector math. In 2D or 3D space we most often work with a Cartesian Coordinate System. With respect to this a 2D point or a vector (we need not to distinguish between them here) is defined by a set of two numbers.

The magnitude of a vector a is it's "length" calculated by Pythagoras' theorem

There are some laws in vector algebra, instructing how to negate, add, subtract, and multiply vectors.

There is a problem though with the vector product (cross product), since it is only defined for 3D vectors. As a way out of this we want to introduce the orthogonal operator.

When applying the orthogonal operator to a vector a, we yield the vector a^{^}, which is orthogonal — i.e. perpendicular — to the original vector.

It's easy to proof, that a^{^} is orthogonal to a, as the dot product of these two must be zero.

When we multiply a vector a with another orthogonal vector b^{^}, the result

is identical to the z-coordinate of the result of cross product

This equivalence will be of some help later. Now let's have a look at some rules with this orthogonal operator.

(1) a^{^} =  a_y−a_x 

(2) a^{^^} = −a

(3) (a + b)^{^} = a^{^} + b^{^}

(4) a^{^} · b^{^} = a · b

(5) a^{^} · b = − a · b^{^}

(6) a · a^{^} = 0

In 2D vector graphics it is desirable to generally avoid trigonometric functions, as these are quite computation intensive. The above formulas build a good foundation to approach this goal.

In order to avoid angles we start to discuss them first. A 2D vector can be decomposed into it's magnitude and unit vector.

The unit vector can be expressed by sin and cos of its angle to the positive x-axis.

This unit vector obviously has the required magnitude of "1", since

Now consider another vector

The dot product yields

Using the addition theorem of trigonometry this equation can be rewritten as

simultaneously introducing the angle φ = β − α from vector a to vector b.

In a similar manner we calculate the dot product

and apply again the addition theorem of trigonometry

Equations (7) and (8) can be taken as the basis for rather efficient expressions of the trigonometric functions of an angle φ between two vectors a and b.

(9) sin φ = a· b^{^}a · b = a_x b_y − a_y b_xa · b

(10) cos φ = a · ba · b = a_x b_x + a_y b_ya · b

(11) tan φ = a· b^{^}a · b = a_x b_y − a_y b_xa_x b_x + a_y b_y

with

a · b = √(a2x + a2y) · √(b2x + b2y)

The above formulas are very convenient in case of two given vectors and the requirement to use trigonometric functions of the angle φ between them for continuative calculation.

If you really need the angle φ itself, I strongly recommend to use equation (11) , which is

• most efficient, since there is no square root to be calculated.
• supported by nearly all programming languages via their atan2 function, which takes into consideration the angle's sign corresponding to the associated quadrant.