|2005-12-20| e3 # Klausur vom 4.02.2004 Aufgabe 1
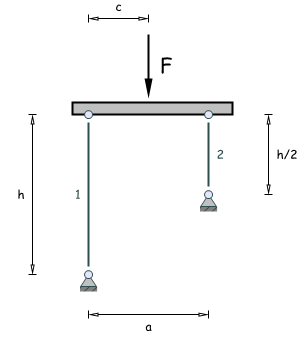Ein starrer Balken wird durch eine vertikale Einzelkraft F = 1 kN belastet. Zwei senkrechte, elastische Stäbe mit identischen Querschnitts- und Materialeigenschaften sowie unterschiedlichen Längen stützen den Balken.
Geg: E = 1.0·104 Nmm2; A = 50 mm2; h = 0.1 m; a = 20 cm
- Ermitteln Sie die Balkenschiefstellung (in Grad) bei mittigem Kraftangriff.
- An welcher Stelle c des Balkens muss die Kraft angreifen, damit der Balken horizontal bleibt ?
Lösung:
a)
∑ Fy ≡ s1 + S2 − F = 0
∑ MA ≡ S2·a − F·a2 = 0
S2 = F·a2a = F2
S1 + S2 = F
S1 = S2 = 12·F = 12 kN
Δli = Si·lE·A
Δl1 = 12·103 N · h1·104 Nmm2·50mm2 = 1·103 N · 100mm·mm22·104 N · 50mm2 = 0,1 mm
Δl2 = 1·103 N · h22·104 Nmm2·50mm2 = 1·103 N · 100mm·mm22·104 N · 50mm2·2 = 0,05 mm
Schiefstellung
Δlges = Δl1 − Δl2 = 0,1 mm − 0,05 mm = 0,05 mm
tanα = 0,05mm200mm = 0,00025
α = 0,014°
b)
∑ Fy ≡ S1 + S2 − F = 0
∑ MA ≡ S2·a − F·c = 0
S2 = F·ca
S1 = F − F·ca = F(1−ca)
Δl1 = Δl2
S1·hE·A = S2·h2·E·A
F·(1 − ca) · hE·A = F·c·h2a·E·A
1 − ca = c2a
2a − 2c = c
c = 23·a = 13,33 cm
|2005-12-20| e4 # Klausur vom 07.07.2004 Aufgabe 1
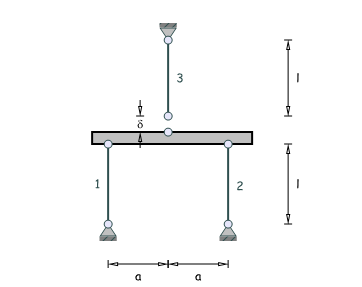Ein dritter Stab (3) soll ungeachtet des Fertigungsfehlers δ zusätzlich an einen starren Balken angeschlossen werden. Wegen der statischen Überbestimmtheit sind nach der Montage die Stabkräfte S1, S2, S3 zu beobachten. Wie gross sind diese?
Geg: δ = 2 mm; A = 12 mm2; l = 1.0 m;
E = 10000 Nmm2; a = 20 cm
Lösung:
S1 + S2 = S3 ⇒ S3 = 2·S1
Δl12 + Δl3 = δ
Δl3 = S3·lE·A
Δl12 = S3·l2·E·A
δ = S3·lE·A+S3·l2·E·A= 32·S3·lE·A
S3 =δ·2·E·A3·l=2mm·2·10000N·12mm23·1000mm·mm2
S3 = 160 N
Δl12 = S1·lE·A
Δl3 = 2·S1·lE·A
δ = S1·lE·A+2·S1·lE·A=3·S1·lE·A
S1 = δ·E·A3·l=2mm·10000N·12mm23·1000mm·mm2
S1 = S2 = 80 N
|2005-12-20| e5 # Klausur vom 02.02.2005 Aufgabe 3
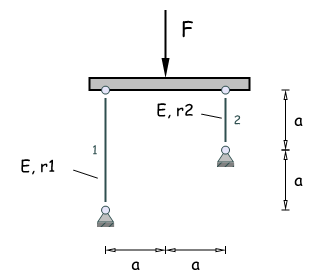Ein horizontaler, starrer Balken ist auf zwei vertikalen, elatischen Stäben mit Kreisquerschnitten verschiedener Radien, unterschiedlicher Länge und gleichen Materials gelagert.
Geg: F = 500 N, a = 40 cm, E = 105 Nmm2
- Wie ist das Radienverhältnis r1/ r2 zu wählen, damit der mittig belastete Balken auch nach der Belastung horizontal bleibt?
- Welchen Radius r1 muss der längere Balken bei einer Knicksicherheit Sk = Fk/F=2 erhalten?
Lösung:
a)
Δl = F·lE·A
A = π·r2
Δl1 = F·2aE·π·r21
Δl2 = F·aE·π·r22
Δl1 = Δl2
F·2aE·π·r21 = F·aE·π·r22
2r21 = 1r22
r1 = r2 · √2
r1r2 = √2
b)
S1 = F2
2·S1 = π2·E·π·r44·(2a)2
r = (F·16·a2π3·E)1/4
r = (500N·16·(400mm)2·mm2π3·105 N)1/4
r = 4,51 mm
woher weiss ich, dass ich, das ich bei b) für Imin, Ixx/Iyy und nicht Ip nehmen muss???
|2005-12-20| e6 # Klausur vom 14.03.2005 Aufgabe 3
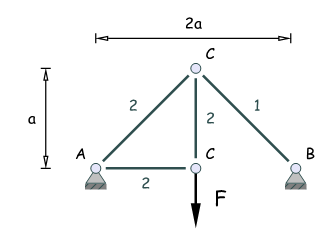Welchen Durchmesser muss der Kreisquerschnitt des Fachwerkstabes 1 mindestens erhalten, damit dieser die 2-fache Sicherheit gegen Knicken (Euler) besitzt?
Geg: F = 1 kN, a = 100 cm, E = 105 Nmm2
Lösung:
Lagerkräfte
∑ Fx ≡ Ax − Bx = 0
∑ Fy ≡ Ay + By − F = 0
∑ MA ≡ By·2a − F·a = 0
By = F2 = 500 N
Ay = F2 = 500 N
Ax = Bx
Stabkraft
∑ Fy ≡ 500 N + 12·√2·S1
S1 = −500N12·√2 = −707,11 N
S1 = 707,11 N
Sicherheit gegen Knicken nach Euler
FK = 2·S
lk = √2 · a = √2 · 1000 mm
I = 14·π·r4
FK = π2·E·Iminl2K
2·707,11 N = π2·105 N·π·r4mm2·4·2·(1000mm)2
r =(2·707,11 N·4·2·(1000mm)2·mm2105 N·π3)1/4
r = 7,77 mm
d = 15,54 mm
Bitte folgende Vorgehensweise wählen:
- Nachweis, dass
Stab 1der horizontale Stab Nullstab ist. - Knotenschnitt Knoten C.
…
(sg)oder mann nimmt sich Regel 2: "2 nicht gleichgerichtete Stäbe an einem belastetem Knoten, wobei die Kraft in Richtung eines Stabes verläuft, so ist der andere ein Nullstab" !!
|2005-12-20| e7 # Klausur vom 06.07.2005 Aufgabe 3
Drei Rundstäbe aus identischem Material sind gemäß Skizze gelagert. Im Fall I liegt Spannungsfreiheit vor. Im Fall II haben sich die Einspannstellen durch thermische Einflüsse um den Betrag Δl verschoben.
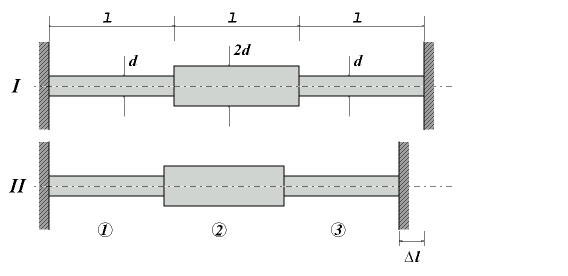
Ermitteln Sie:
- die Kräfte in den Einzelstäben 1, 2, 3.
- die Spannungen in den Einzelstäben 1, 2, 3.
Lösung:
a)
S = S1 = S2 = S3
Δl = Δl1 + Δl2 + Δl3
Δli = S·lE·Ai
Δl = 4·S·lE·π·d2+S·lE·π·d2+4·S·lE·π·d2
Δl = 9·S·lE·π·d2
S = Δl·E·π·d29·l
b)
σi = SAi
σ1 = σ3 = 4·Δl·E9·l
σ2 = Δl·E9·l
|2006-01-12| e8 # Übungsaufgabe vom 26.10.2005
Ein starrer Balken hängt an zwei elastischen Stäben mit unterschiedlichen Durchmessern d2 =2 · d1
Geg:
d1 = 5mm
E = 1,0 · 105 Nmm2
F = 10 kN
l = 1,5 m, a = 0,5 m
Ges:
a)Schiefstellung des Balkens in [Deg]
b)Wohin muss die Kraft F verlagert werden, wenn der Balken horizontal bleiben soll?
a)
Stab 1:
A1 = π4 · d1 2 = π4 · (5mm)2 = 19,635 mm2
F1 = 5kN
σ1= 5000N19,635 mm2 = 254,65 Nmm2
ε1 = σ1E = 254,65 Nmm21,0 · 105 Nmm2 = 2,5465 · 10−3
Δ l1 = E1 · l = 2,5465 · 10 · 1,5 m = 3,82 mm
Stab 2:
A2 = π4 · d2 2 = π4 · (10mm)2 = 78,54 mm2
F2 = 5kN
σ2= 5000N78,54 mm2 = 63,66 Nmm2
ε2 = σ1E = 63,66 Nmm21,0 · 105 Nmm2 = 6,366 · 10−4 · 10−3
Δ l2 = E2 · l = 6,366· 10−4 · 1,5 m = 0,955 mm
Δ l = Δ l1 − Δ l2 = 2,865 mm
tan α = 2,8651000 = 2,856 · 10−3
α = 0,164°
b)
∑ Fy ≡ −F + S1 + S2 = 0
∑ M1 ≡ − F · e + S2 · 2a = 0
S2 = F · e2·a
S1 = − F · a2·a + F = F·(1 − e2·a)
ε1 =!ε2 ⇒ S1E · A1 = S2E · A2
(1 − e2a) · 4π·d2 = e2·a·π+d2
4 − 4e2·a = e2·a
8a − 4e = e
8·ae −4 =1
8·ae =5
e = 85·a
Wobei e die Strecke vom linken unteren Endpunkt des Balkens bis zum Angriffspunkt der Kraft repräsentiert! e setzt eigentlich bei mittlerer Stärke des linken Balkens an.
|2006-01-12| e9 # Übungsaufgabe vom 02.11.2005
Berechnung einer Staberwärmung
Geg:
l = 250mm, A = 700 mm2
s = 0,5 mm
E = 2,1 · 105 Nmm2
αT = 1,2 · 10−5 K−1
Ges:
a) Staberwärmung Δ T1 für Kontakt mit der rechten Wand
b) Staberwärmung Δ T2 bis 80% der Streckgrenze RP0,2 = 500 Nmm2 innerhalb des Stabes wenn die Spannung erricht wird.
a)
εtherm = αT · Δ T1 = sl
εmech = σE
εtherm = αT · Δ T1
Δ T1 = sαT · l
Δ T1 = 0,5 mm1,2 · 10−5 K−1 · 250 mm = 166,67 K
b)
εtherm − εmech = sl
αT · Δ T2 − 0,8 · RP0,2E = sl
Δ T2 = ( sl + {0,8 · RP0,2} · 1α T
Δ T2 = ( 0,5250 + 0,8 · 5002,1 · 105) · 11,2 · 10−5 K
Δ T2 = 325 K
|2006-01-12| e10 # Übungsaufgabe 1 vom 27. 10. 05
Ein Rohr wird auf Zug belastet
Gegebene Größen sind:
der Außendurchmesser Ø 20 mm
die Zugkraft F = 13,5 kN
die zulässige Spannung σzul =80 Nmm2
Gefragt wird nach dem Innendurchmesser d:
σ = FA
⇒ A (Querschnittsfläche) = FQ
A = 13500 N80 Nmm2
A = 168,75 mm2
Man zieht nun einfach die neue Querschnttsfläche von der geg. Querschnittsfläche = 314,16 mm2, errechnet aus dem gegebenen Durchmesser 20mm ab und erhält somit die Innenfläche:
314,16 − 168,75 = 145,41
145,41 = r2 π | /π
√145,41 π = r
⇒d = 13,6 mm
|2006-01-12| e11 # Übungsaufgabe 2 vom 27.10.05
Ein Gummiseil soll von 5m auf 6m verlängert werden.
Geg:
F = 1 kN
E = 8 Nmm2
Ges:
a) Spannung
b) Seil Ø
a)
σ = E · ε
ε = Δ ll
σ = 8 Nmm2 · 15
= 85 Nmm2
= 1,6 Nmm2
b)
σ = FA
⇒ A = 1000 N1,6 Nmm2
A = 625 mm2
625mm2 = r2 · π
√ 625π = r
14,1 = r
d = 28,2 mm
|2006-01-12| e12 # Übungsaufgabe 3 vom 27.10.05
Eine Stahlstange hängt frei herab und ist am unteren Ende mit einer Last G beanschlagt.
Gegebene Größen:
l = 80 m
Ød = 16 mm
G = 22 kN
Gesucht wird:
a) die Spannung am oberen Ende (mit Eigengewicht)
b) die Verlängerung auf Grund der Belastung (ohne Eigengewicht) und
c) die Verlängerung mit Eigengewicht.
a)
Eigengewicht = 800 dm · A · 7,8 kgdm3
= 125 kg
= 1226 N
mit A = 0,020106 dm3
Gesamtgewicht: 23226 N
σ = FA = 23226 N201,06 mm2 = 115,6 Nmm2
b)
ε = Δll
Δl = ε · l
σ = FA = E · ε
ε = FA · E = 12000 N201,06 mm2 · 2,1 · 105 Nmm2
ε = 5,21 · 10−4
Δl = ε · l = 0,0416 m ⇒ 41,6 mm
c)
ΔlEigen = m · g · l2E · A = 1226 N · 80 · 103 mm2 · 2,1 · 105 Nmm2 · (8mm)2 · π
= 1,16 mm
|2006-01-19| e13 # Übungsaufgabe 4 vom 27.10.05
Zugbolzen
Berechnet werden soll der Durchmesser d (mit der Formel für die Flächenpressung P = FA)und die Kraft F, der/die zu den gegebenen Spannungs-/ und Flächenpressungs-Grenzwerten passt!
Geg:
Ø D = 50 mm
σzul = 80 Nmm2
Pzul = 60 Nmm2
Ges:
F, d
Pzul = FAKopf ⇒ F = Pzul · AKopf
σzul = FASchaft ⇒ F= σzul · ASchaft
⇒
Pzul · AKopf = σzul · ASchaft
mit
AKopf = π4 · ( D2 − d2)
ASchaft = π4 ·d2
Pzul · π4 · (D2 − d2) = σzul · π4 d2
d2 (σzul + Pzul ) = Pzul · D2
d = D · √ (Pzulσzul + Pzul)
d = 50 mm · √(60140) = 32,7 mm
Wenn man nun d in z. B. F = Pzul · AKopf einsetzt erhält man:
F= 67,420 kN
