Von der bislang rein axialen Belastung des Stabes wollen wir nun zu einer Belastung senkrecht zu dessen Achse bzw. zur Beanspruchung durch ein Biegemoment übergehen. Der Stab wird durch diese Lastannahmen zum Balken.

In Anlehnung an die praxisübliche Vorgehensweise vereinbaren wir zunächst folgende

idealisierende Annahmen:

• Die Dehnung und Verdrehung aller Körperelemente sind sehr klein gegenüber den Balkenabmessungen, daher werden alle Kräfte am unverformten Balken angesetzt (Linearisierung).
• Der Werkstoff sei homogen und isotrop, deshalb gilt das verallgemeinerte Hooke´sche Gesetz.
• Die Querschnittsabmessungen seien deutlich kleiner als die Balkenlänge^{15Diese Formulierung entspricht der bereits bekannten Definition eines Balkens.}.
• Die Balkenachse ist Verbindungslinie aller Querschnittsflächenpunkte.
• Die Balkenachse sei im unbelasteten Zustand gerade, d.h. nicht gekrümmt.
• Äußere Kräfte wirken entlang einer Hauptträgheitsachse und äußere Momente drehen ebenfalls um eine Hauptträgheitsachse der Balkenquerschnittsfläche (gerade Biegung)^{16Der allgemeine Fall der schiefen Biegung besitzt diese Einschränkung nicht.}.

Voraussetzung

Unter der Belastung eines Balken durch reine Biegung verstehen wir die zugehörigen Schnittgrößenverläufe:

N(z)=0 (keine Normalkraft)

Q(z)=0 (keine Querkraft)

M(z)=const (konstantes Biegemoment)

Beispiele reiner Biegebelastung

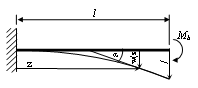
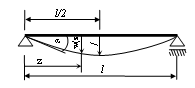
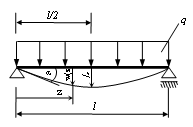
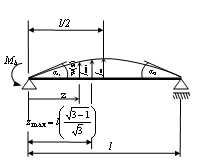
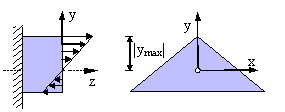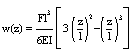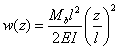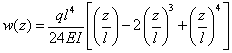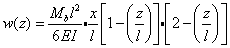Durch das Herauschneiden eines Balkenstücks

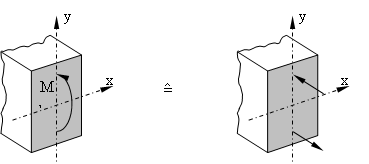
wirkt auf die so erzeugte Querschnittsfläche als Schnittgröße lediglich ein Biegemoment um die x-Achse. Diese Moment ist einem Kräftepaar äquivalent und bewirkt im oberen Bereich des Querschnitts eine Druckspannung sowie im unteren Bereich eine Zugspannung.

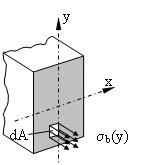
Zu einer genaueren Aussage gelangen wir, indem wir die durch die Biegung erzeugte Normalspannung eines differentiell kleinen Flächenstücks dA betrachten. Die resultierende Kraft in diesem Flächenstück ist σ_b(y)·dA. Damit formulieren wir die

1. Verträglichkeitsbedingung

Die Biegespannung hat keine resultierende Kraftwirkung, d.h.

 ∫A·σ_b(y)·dA = 0

Weiterhin gibt es kein resultierendes Moment um die y-Achse und damit gilt die

2. Verträglichkeitsbedingung

Die Biegespannung erzeugt kein resultierendes Moment um die y-Achse, d.h.

 ∫A·xσ_b(y)·dA = 0

Schließlich muß die Biegespannung ein Moment um die x-Achse der Größe M_b erzeugen, damit haben wir die

3. Verträglichkeitsbedingung

Die Biegespannung resultiert in einem Moment M_b um die x-Achse, d.h.

 ∫A·yσ_b(y)·dA = M_b

Diese bis hierher aufgestellten Bedingungen reichen immer noch nicht aus, um den Biegespannungsverlauf über der Querschnittsfläche zu bestimmen. Daher betrachten wir in einem weiteren Schritt ein verformtes Balkenstück.

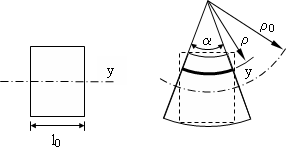
und berücksichtigen bei der angenommenen Verformung die

Bernoulli-Hypothese der Biegetheorie

Die Querschnitte eines Balkens bleiben auch während der Biegeverformung eben und senkrecht zur (gekrümmten) Balkenachse.

In unserem speziellen Fall einer Belastung durch ein konstantes Biegemoment über die gesamte Balkenachse hat diese an jeder Stelle die gleiche Krümmung und geht daher in einen Kreisbogen über.

Am verformten Balkenstück kann dann jeder y-Koordinate eine Faser der Form konzentrischer Kreisbögen zugeordnet werden. Diese liegen im Abstand ρ(y) zum Krümmungsmittelpunkt und sind im "oberen Bereich" gegenüber der Ausgangslänge l₀ verkürzt und im "unteren Bereich" gelängt. Im Übergang zwischen diesen beiden Bereichen muß es eine sog. neutrale Faser der Länge l₀=α·ρ₀ geben.

Aufgrund des Ebenbleibens der Querschnitte liegt dann eine lineare Dehnungsverteilung vor, d.h.

lineare Dehnung

ε(y)= −yρ₀

Zwischen der Spannung und Dehnung besteht ebenfalls ein linearer Zusammenhang.

(Hooke´sches Gesetz) womit wir die Spannungsverteilung

über der Querschnittsfläche als Geradengleichung erhalten. Nun ist noch die Lage (Nullpunkt) und Steigung der Geraden (ρ₀) unbekannt.

Wir setzen die Geradengleichung der Spannungsverteilung in die 1. Verträglichkeitsbedingung ein und erhalten

und damit

als Forderung, daß das Flächenmoment 1. Ordnung bezüglich der x-Achse verschwindet. Diese erfüllt nur der Flächenschwerpunkt.

Als Ergebnis stellen wir also fest, daß der x,y-Koordinatenursprung in dem Querschnittsflächenschwerpunkt liegt. Hinsichtlich der Steigung der Geradengleichung benutzen wir die 3. Verträglichkeitsbedingung und erhalten

und mit

(Flächenmoment 2. Ordnung bezügl. der x- Achse)
läßt sich diese Beziehung nach dem Krümmungsradius ρ₀ auflösen

Damit erhalten wir nunmehr durch Einsetzen von ρ0 in die lineare Spannungsverteilung, die

Gleichung der Biegespannung

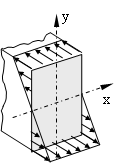
σ_b(y)=M_bI_xx·y

Mit M_b = konstantes Moment
I_xx = entlang der Balkenachse gleichbleibendes Flächenmoment

Interessenhalber setzen wir die Gleichung der Spannungsverteilung noch in die 2. Verträglichkeitsbedingung ein und erhalten mit

die Bedingung, daß das Deviationsmoment

verschwindet. Dies ist gleichbedeutend damit, daß die x,y-Achsen gleichzeitig Hauptträgheitsachsen sind.
Die Spannungsgleichung ist demnach nur unter dieser Voraussetzung gültig. Andernfalls ist nach den Formalismen der schiefen Biegung zu rechnen.

Durch die nun wirkenden Querkräfte werden in einer Schnittfläche des Balkens zusätzlich zu den Biegespannungen Schubspannungen erzeugt (s. Abschnitt 7). Diese Spannung wollen wir hier nicht berücksichtigen. Da das Biegemoment und gegebenfalls die Querschnittsabmessungen über z variieren, müssen wir die

Gleichung der Biegespannung für veränderliches Biegemoment und Flächenträgheitsmoment

σ_b(y,z)=M_b(z)I_xx(z)·y

Mit M_b(z) = variables Biegemoment

I_xx(z) = variables Flächenmoment

verwenden.

Wenn die bislang erfüllte Forderung, daß die Biegeachse^{17Achse, um die das Biegemoment dreht.} eine Hauptträgheitsachse des Querschnitts ist, nicht mehr eingehalten werden kann, so sprechen wir von einer schiefen Biegung.

Da jede Fläche zwei senkrecht aufeinanderstehende Hauptträgheitsachsen besitzt, kann das Biegemoment in zwei Komponenten in Richtung eben dieser Achsen aufgeteilt werden. Die resultierende Biegespannung ergibt sich dann aus der Überlagerung dieser geraden Biegungsfälle.

Gleichung der Biegespannung für schiefe Biegung^{18auch zweiachsige Biegung}

σ_b(x,y,z)=M_bx(z)I_xx(z)·y + M_by(z)I_yy(z)·x

Ziel der Spannungsberechnung ist der Nachweis der Festigkeit eines Balkens in der Form, daß an keiner Stelle des Balkens und in keinem Flächenstück des Balkenquerschnitts die zulässige Spannung überschritten wird. Wir nennen dies den Spannungsnachweis. Um die Vorgehensweise näher zu beleuchten, betrachten wir einen eingespannten Balken mit Dreiecksquerschnitt.

Nun wollen wir die Forderung nach einem konstanten Biegemoment ebenso wie die Bedingung eines konstanten Querschnitts entlang der Balkenachse fallenlassen und die Biegespannung aufgrund äußerer Kräfte bzw. Streckenlasten untersuchen.

Das größte Biegemoment tritt in diesem Fall an der Einspannstelle (z=0) auf. Eine Skizze des Spannungsverlaufs über den Querschnitt an dieser Stelle

verdeutlicht, daß die betragsmäßig größte Spannung an der oberen Faser auftritt. Dies ist gleichzeitig der Randpunkt des Querschnitts mit dem größten Abstand ymax vom Schwerpunkt. Die größte Biegespannung erhalten wir demnach aus der Beziehung

Da sowohl I_xx als auch y_max reine Flächenkenngrößen sind, werden diese häufig zusammengefaßt und bilden gemeinsam das sogenannte

Widerstandsmoment

W_x = I_xx|y_max| ; W_y = I_yy|x_max|

• bezieht sich immer auf Hauptachsen
• hat Dimension "Länge hoch 3"
• ist ein Maß für die Festigkeit eines Querschnitts gegenüber einer Biegebelastung
• darf nicht mit einem anderen Widerstandsmoment addiert werden
• läßt die Information hinsichtlich Zug-/Druckbelastung aufgrund des Betrages verschwinden

Für den Spannungsnachweis eines Balkens muß also die Bedingung

für alle Querschnitte erfüllt sein. Für die Querschnittswahl (Dimensionierung) eines Biegebalkens läßt sich demgegenüber die Beziehung

verwenden, um das erforderliche Widerstandsmoment zu bestimmen.

Beispiel

Ein Balken mit linear veränderlicher Höhe h und konstanter Breite ist am linken Rand fest eingespannt und wird am rechten Rand durch eine senkrechte Einzelkraft F belastet. Frage:

• An welcher Stelle tritt die minimale Biegespannung auf? Geg.:

• Für welchen Höhenverlauf h(z) der Balkenfaser ist die maximale Biegespannung in jedem Querschnitt gleich? Lösung:
• Bei einer linear veränderlichen Höhe gilt die Funktion

Als Flächenträgheitsmoment kennen wir

und bestimmen das Widerstandsmoment zu

Der ebenfalls lineare Biegemomentverlauf gehorcht der Beziehung

Damit erhalten wir für die Biegespannung

Das Maximum dieser Funktion gewinnen wir durch die Ableitung nach z

und Auffinden deren Nullstelle.

also

bzw. mit

• Mit
  

und

ergibt sich

Voraussetzungen

Ein Balken erfährt aufgrund einer Belastung senkrecht zu seiner Achse neben inneren Spannungen auch eine Verformung.

Als Voraussetzung behalten wir die getroffenen Vereinbarung - Querschnitte bleiben eben und senkrecht zur Balkenachse (Bernoulli-Balken) - weiterhin bei.^{19Diese Forderung führt zu einem schubstarren Balken, d.h. einem Balken, der keine Schubverformung erleidet.}

Differentialgleichung der Biegelinie

Zur Herleitung des Biegemoments im Abschnitt Biegespannungen haben wir bereits die Biegeverformung berücksichtigt.

Wir knüpfen daran an und verwenden zunächst die Gleichung der Biegespannung

sowie die Aussage hinsichtlich einer linearen Spannungsverteilung gemäß

Die Kombination dieser Gleichungen führt auf

eine Beziehung zwischen der Biegemomentbelastung eines Balkens und der Krümmung der Balkenachse (neutrale Faser).

Die Krümmung 1ρ_o der Balkenachse ist proportional zum Biegemoment

M_b(z)=E·I_xx(z)·1ρ_o

Der Faktor E·I wird dabei als Biegesteifigkeit bezeichnet.

Die Verschiebung w(z) eines beliebigen Punktes der Balkenachse habe dabei die gleiche Richtung wie die y-Achse.^{20Häufig wird die Verschiebung w in negative y-Richtung angesetzt.}

Es besteht nun ein mathematischer Zusammenhang zwischen der Krümmung einer beliebigen Kurve (im y,z-System) und der y-Koordinate gemäß

mit

Wir setzen diese Krümmungsgleichung unter Verwendung von w statt y in unsere obige Beziehung ein und erhalten die

Differentialgleichung der Balkenbiegung

E·I_xx(z)·w″(1+w′²)²³ = M_b

Diese Differentialgleichung ist nichtlinear und in dieser Form für die praktische Arbeit des Ingenieurs kaum brauchbar.
Glücklicherweise treffen wir in der technischen Praxis hauptsächlich sehr kleine Durchbiegungen an, weswegen wir das quadratische Glied w´² gegenüber 1 vernachlässigen können.^{21Bei einem Anstieg von 5° liegt der Fehler noch unter 1%.} Daher arbeiten wir bei kleinen Verformungen mit der

Differentialgleichung 2. Ordnung der Biegelinie

E·I·w″ = M_b

In dieser - nun linearen inhomogenen gewöhnlichen - Differentialgleichung 2. Ordnung können neben der Durchbiegung w auch das Biegemoment M_b sowie die Biegesteifigkeit E·I von z abhängig sein.

Mit den von den Schnittgrößen bekannten Zusammenhängen

zwischen Streckenlast, Querkraft und Biegemoment erhalten wir schließlich die allgemeine

Differentialgleichung 4. Ordnung der Biegelinie

(E·I·w″) ″ = −q

oder bei konstanter Biegesteifigkeit E· I

E·I·w″ ″ = −q

Lösung der Biegeliniengleichung

Durch die Biegeliniengleichung wird ein Randwertproblem beschrieben. Die Lösung w(z) erhalten wir, indem wir die Differentialgleichung zweimal (2. Ordnung) oder viermal (4. Ordnung) integrieren. Die zwei bzw. vier Integrationskonstanten müssen dann mit Hilfe von Randbedingungen bestimmt werden.
Hinsichtlich der Entscheidung, welche Differentialgleichung (2. oder 4. Ordnung) zur Lösung eines Problems heranzuziehen ist, gilt die

Regel für die Wahl der Biegeliniengleichung

Biegeliniengleichung 2. Ordnung:

kann bei statisch bestimmten Balkenproblemen benutzt werden, wenn der Biegemomentenverlauf vorher bestimmt wurde.

Biegeliniengleichung 4. Ordnung:

kann jederzeit benutzt werden, auch ohne Bestimmung des Biegemomentenverlaufs; muß grundsätzlich bei statisch überbestimmter Balkenlagerung herangezogen werden.

Wenn möglich sollte der einfacheren Differentialgleichung 2. Ordnung der Vorzug gegeben werden.

Die Vorgehensweise werde an folgendem einfachen Beispiel demonstriert.

Ein Balken konstanter Biegesteifigkeit E·I sei am linken Rand (Koordinatenursprung) eingespannt und am rechten Ende durch eine senkrecht nach unten wirkende Einzelkraft F belastet. Wir ermitteln die Biegelinie Ein Balken konstanter Biegesteifigkeit E·I sei am linken Rand (Koordinatenursprung) eingespannt und am rechten Ende durch eine senkrecht nach unten wirkende Einzelkraft F belastet. Wir ermitteln die Biegelinie

2 Ordnung	4 Ordnung
EIw″= −F(l−z) EIw′= −F(lz−l22)+c1 EIw= −F (12 z2 − z36)+c1 z+c2	EIw″″ = 0 EIw″′ = c1 EIw″ = c1 z+c2 EIw′ = 12 c1 z2 + c2 z + c3 EIw = 16·c1 z3+ 12 c2 z2+c3 z+c4
Randbedingungen: ψ(z=0) = w′(z=0) = 0 ⇒c1 = 0 w(z=0) = 0 ⇒c2 = 0 w=− F2EI·(lz2 − z33 )	Randbedingungen: Q(z=l)=EIw″′(z=l) = −F ⇒c1 = −F Bb(z=l)=EIw′(z=l)= 0 ⇒c2 = F·l ψ(z=0)=w′(z=0) = 0 ⇒c3=0 w(z=0)=0 ⇒c4 = 0 w = F2EI (z33 −lz2)

An diesem Beispiel wird der notwendige Mehraufwand bei der Gleichung 4. Ordnung deutlich.

Für einen statisch überbestimmt gelagerten Balken wollen wir ebenfalls die Biegelinie ermitteln. Da es hierbei nicht möglich ist, Lagerreaktionen und Schnittgrößen zu bestimmen, müssen wir die Differentialgleichung 4. Ordnung der Biegelinie heranziehen. An diesem Beispiel wird der notwendige Mehraufwand bei der Gleichung 4. Ordnung deutlich.

Für einen statisch überbestimmt gelagerten Balken wollen wir ebenfalls die Biegelinie ermitteln. Da es hierbei nicht möglich ist, Lagerreaktionen und Schnittgrößen zu bestimmen, müssen wir die Differentialgleichung 4. Ordnung der Biegelinie heranziehen.

Die Randbedingungen lauten

Dies führt auf vier Bestimmungsgleichungen für die vier Integrationskonstanten

und führen auf die Gleichung der Biegelinie

Darüber hinaus haben wir auch den Querkraft- und Momentenverlauf gewonnen

Zur Festlegung der Randbedingungen bei Biegeproblemen ist folgende Übersicht hilfreich.

Lagerung	w	w′	M	Q
	0	-	0	-
	-	0	-	0
	0	0	-	-
freies Ende	-	-	0	0

Randbedingungen für die Integration der Biegegleichung.

Wirken auf einen Balken mehrere Lastfälle, d.h. Einzelkraft, Streckenlast oder Moment, so lassen sich die Durchbiegungen aufgrund der einzelnen Lastfälle überlagern und somit summieren.

Diese Möglichkeit der Überlagerung oder Superposition der Einzelverschiebungen ist allein wegen der Linearität der Differentialgleichung gegeben. Eine Superposition läßt sich nicht nur auf die Verschiebung w , sondern auch auf alle Ableitungen von w anwenden, also:

w = w₁+w₂ (Verschiebung)

w′ = w′₁+w′₂ (Neigung)

M_b = M_b1+M_b2 (Momentenverlauf)

Q = Q₁+Q₂ (Querkraftverlauf)

q = q₁+q₂ (Streckenlast)

Eine Vereinfachung für die Ermittlung von Durchbiegungen ergibt sich durch die Bereitstellung einer Biegelinientafel mit einfachen Lastfällen.

Beispiel:

Ein Balken ist in A, B gelagert und wird mit den Kräften F₁ und F₂ belastet Es sind w₁ und w₂ zu ermitteln.

Geg.: F₁=2F, F₂=F,l mit w₁=w₁₁+(-w₁₂) Wir benutzen Lastfall 1 mit Kraft F₁ an Stelle 1 mit Hilfe der Biegelinientafel 6.5/ Belastungsfall 4 und erhalten die Gleichung der Biegelinie

Zusätzlich benötigen wir Lastfall 2 mit Kraft F₂ an Stelle 2 mit Hilfe der Biegelinientafel 6.5/ Belastungsfall 4 und erhalten eine weitere Gleichung der Biegelinie

Wir betrachten einen Rahmen als ein Gebilde aus winklig zueinander zusammengesetzten Balken. Auf einen solchen Rahmen kann das Prinzip der Superposition ebenfalls angewendet werden.

---

Beispiel:

Ein Rahmen wird durch ein Kräftepaar belastet.

Gesucht ist die horizontale Verschiebung der unter F angreifenden Kraft:

Wir ermitteln 3 Lastfälle und erhalten folgende Überlagerungen

mit

• w₁ = 23·a·φ
• w₂ = 23·a·ψ

Wir benutzen Lastfall 1 mit Hilfe der Biegelinientafel 6.5/ Belastungsfall 1 und erhalten die Durchbiegung mit

weiterhin Lastfall 2 (Biegelinientafel 6.5/ Belastungsfall 2) mit

und schließlich Lastfall 3 (Biegelinientafel 6.5/ Belastungsfall 3) mit

mit den Überlagerungen der Lastfälle 1-3 erhalten wir als Ergebnis

Das Superpositionsprinzip erlaubt uns auch, die Auflagerkräfte von überbestimmt gelagerten Balken und Rahmen zu ermitteln. Dabei wird die Lagerkraft in einem Lastfall als unbekannte Kraft angesetzt und in den restlichen Lastfällen einfach ignoriert. Beispiel:

mit

• w₁ = φ·l
• w₂ = ψ·l
• w₃

(Biegelinientafel 1, Lastfall 1)

(Biegetafel 1, Lastfall 2)

(Biegetafel 1, Lastfall 3)