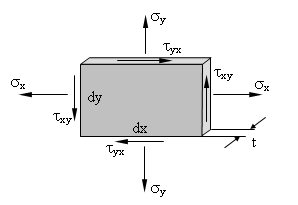
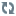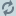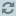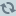Wir wollen nun untersuchen, welche Spannungen in einer beliebigen Schnittfläche des Bauteils wirken. Die Seiten des betrachteten herausgeschnittenen Rechtecks liegen ja parallel zu den Koordinatenachsen - eine spezielle und andererseits recht willkürliche Wahl. Bei der Betrachtung der Spannungen in einer beliebig gerichteten Schnittfläche interessiert insbesondere die Schnittrichtung mit der maximalen Spannung.
Wir schneiden von dem bisherigen Bauteilrechteck ein Stück ab
Durch die Schnittführung unter dem Winkel φ und der neuen Schnittfläche
dA = dl · t
ergeben sich die Flächen der Hypotenusenseiten zu
dAx = dx · t = dl · cosφ · t = dA · cosφ
dAy = dy · t = dl · sinφ · t = dA · sinφ
Die Spannungen der neuen Schnittflächen bezeichnen wir mit σξ und τξη unter Bezugnahme auf ein um φ gegenüber dem x/y-System gedrehten ξ/η -Koordinatensystem.
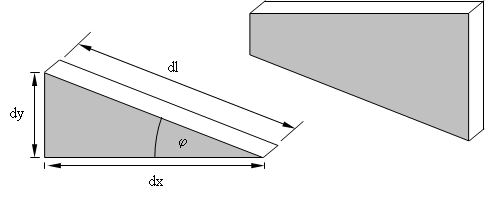
Über die Spannungen an den bekannten Schnittflächen stellen wir die Kräftebilanzen auf.
∑ Fx ≡ (σ×i · sinφ) · A – (τ×iη · cosφ) · A – σx · Ay – τyx · Ax = 0
∑ Fy ≡ (σ×i · cosφ) · A + (τ×iη · sinφ) · A – σy · Ax – τxy · Ay = 0
Eine Multiplikation der ersten Gleichung mit sinφ , der zweiten mit cosφ und anschliessende Summation ergibt
σ×i · dA = σx · sinφ · dAy + σy · cosφ · dAx + τyx · sinφ · dAy + τxy · cosφ · dAy
Analog dazu führt eine umgekehrte Multiplikation mit cosφ und sinφ und Subtraktion der Gleichungen auf
τ×iη · dA = – σx · cosφ · dAy + σy · sinφ · dAx – τyx · cosφ · dAx + τxy · sinφ · dAy
Die Verwendung der gefundenen Beziehungen für die Hypothenusenflächen dAx und dAy in diesen Gleichungen resultiert in den Gleichungen für die Spannungen in der Schnittfläche
σ×i = σx · sin2φ + σy · cos2φ + τyx · sinφcosφ + τxy · cosφsinφ
τ×iη = – σx · sinφcosφ + σy · cosφsinφ · – τyx · cos2φ + τxy · sin2φ
Vollzieht man die vorstehende Betrachtung an einem weiteren Schnitt senkrecht zur gegenwärtigen Schnittführung, ergibt sich eine weitere Gleichung für ση.
Wir erhalten schließlich die
Transformation des ebenen Spannungszustandes auf ein gedrehtes Koordinatensystem
σ×i = σx · sin2 φ + σy · cos2 φ + τyx · sinφ cosφ + τxy · cosφsinφ
σ×i = σx · sin2 φ + σy · cos2 φ + τyx · sinφ cosφ + τxy · cosφ sinφ
τ×iη = (σx − σy)sinφ cosφ + τxy (cos2 φ − sin2 φ)
mit σx, σy, τxy Spannungen im Ausgangskoordinatensystem
σξ, ση, τξη Spannungen im gedrehten Koordinatensystem
Einachsiger Spannungszustand
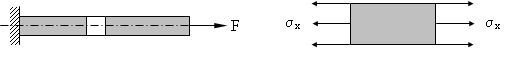
Wenn ein Bauteil ausschließlich durch Normalspannungen in einer Richtung
beansprucht wird, so sprechen wir von einem einachsigen Spannungszustand.
Ein Schnitt durch dieses Bauteilelement unter dem Winkel φ
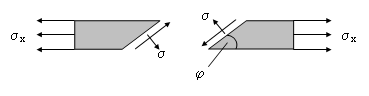
erzeugt in der Schnittfläche sowohl Normal als auch Schubspannungen.
Diese Spannungen ermitteln wir aus den Transformationsgleichungen
des Spannungszustandes, indem wir σ
x und τ
xy = τ
yx = 0 setzen
und und erhalten so die
Transformation des ebenen Spannungszustands
σ×i = σ2φxsin = 12σx(1 − cos2φ)
ση = σ2φxcos = 12σx(1 + cos2φ)
τ×iη = − σxsinφcosφ = − 12σxsin2φ
Die maximalen Schubspannungen treten hier für sinφ = 1 bzw. φ =45° auf.
Hydrostatischer Spannungszustand
Von einem hydrostatischem Spannungszustand sprechen wir, wenn ein Bauteilelement
von allen Seiten mit derselben Normalspannung beanspruchtwird. Die Schubspannungen sind dabei Null.
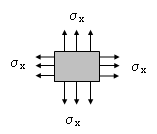
Für diesen Spannungszustand liefern die Transformationsgleichungen für
den hydrostatischen Spannungszustand
σ×i = σ
ση = σ
τ×iη = 0
mit σx = σy = σ, τxy = τxy = 0
Die Spannungen sind hierbei also unabhängig vom Schnittwinkel in allen Richtungen gleich.
Spannungstensor
Die allgemeinen Transformationsgleichungen lassen sich in Matrixschreibweise formulieren
σ×iτ×iητη×iση = cosφsinφ−sinφcosφ · σxτxyτyxσy · cosφ−sinφsinφcosφ
S×iη = RT · Sxy · R
Die Matrix Sxy mit den Spannungen bezeichnen wir als den
Spannungstensor des ebenen Spannungszustands
Sxy = σxτxyτyxσy
mit σx, σy, σxy, σyx = Spannungen am Flächenelement
und τxy, = τyx = Gesetz der zugeordneten Schubspannungen
Zur Transformation wird der Spannungstensor von vorne mit der transponierten
Rotationsmatrix RT und von hinten mit der Rotationsmatrix R multipliziert.
Hauptspannungen
Wir wollen die algebraischen Spannungsgleichungen zunächst etwas umformen.
Dazu verwenden wir die trigonometrischen Beziehungen
sin 2φ = 2sinφ cosφ
cos 2φ = cos2φ − sin2φ
und erhalten
σ×i = 12(σx + σy) + 12(σx − σy)cos2φ + τxysin2φ
ση = 12(σx + σy) − 12(σx − σy)cos2φ − τxysin2φ
τ×i η = − σy) + 12(σx − σy)cos2φ + τxysin2φ
Anhand dieser Gleichungen untersuchen wir nun, für welchen Winkel φ die Normalspannung σ×i
und ση einen Extremwert besitzen. Dazu setzen wir
dσ×idφ = − (σx − σy)·sin2φ + 2τxy·cos2φ = 0
und gewinnen den Winkel zu
tan2φ = 2τxyσx − σy
Gehen wir nun mit diesem Winkel wieder in die obigen Spannungsgleichungen,
so ergeben sich die Extremwerte der Normalspannungen.
Diese bezeichnen wir als
Hauptspannungen des ebenen Spannungszustands
σ1,2 = σx + σy2±√((σx + σy)24) + τ2xy
Der Mohr´sche Spannungskreis
Zu einer geometrischen Veranschaulichung gelangen wir, indem wir die beiden
letzten Spannungsgleichungen im vorangegangen Abschnitt als Komponenten
einer Vektorgleichung auffassen.
σyτxy = 12(σ1 + σ2)0 + 12(σ1 − sigma2) cos2φ∗sin2φ∗
Diese Vektorgleichung ist uns als Kreisgleichung in der Form
P = P0 + r cos2ψsin2ψ
bekannt.
In einem σ/τ -Koordinatensystem liegt dieser Kreis mit seinem Mittelpunkt auf der
σ-Achse (y-Komponente von P0 ist Null) mit dem Abstand ( 12 σ1+σ2) vom Koordinaten-
ursprung und dem Kreisradius 12 (σ1 −σ2).
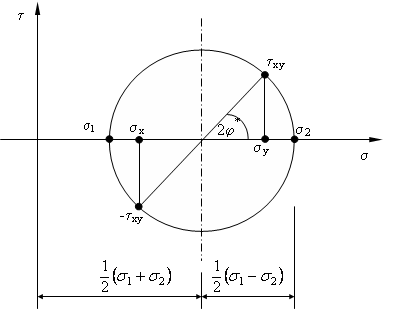
Der Mohr´sche Spannungskreis dient vorwiegend zur Veranschaulichung der Vorzeichen
von Normalspannungen und Schubspannungen an einem Flächenelement.
Dabei ist eine Normalspannung positiv (positive σ-Achse) bei Zug und negativ bei Druck.
Eine Schubspannung ist positiv, wenn ihre resultierende Kraft ein positives Moment um den
Flächenschwrpunkt aufweist, sonst negativ.
Darüberhinaus lassen sich die Spannungen an einem gedrehten Flächenelement (bzw. in einem Bauteilschnitt unter dem Winkel φ ) aus dem Spannungskreis ablesen.