Bislang haben wir die Reaktionskräfte in den Bindungen zwischen starren Körpern untersucht. Den Körpern selbst haben wir zwar die Aufgabe einer Übertragung von Kräften und Momenten zugeschrieben, die Größe und Richtung dieser Kräfte an einer bestimmten Stelle innerhalb des Körpers jedoch nicht näher untersucht. An diese inneren Kräfte gelangen wir, indem wir an der interessierenden Stelle einen geraden Schnitt durch den Körper führen.^{1Eine gerade Schnittführung ist nicht Bedingung, jedoch üblich und hinsichtlich der Ergebnisse ebenso aussagekräftig, ja sogar anschaulicher als ein komplizierter "kurviger" Schnitt.}

Wenn der Körper vor dem Schnitt im Gleichgewicht war, müssen es die entstandenen Körperhälften auch nach dem Schnitt sein. Demnach sind in der Schnittfläche entsprechende Reaktionskräfte analog zum Freischneiden von Bindungen anzutragen. Diese Reaktionskräfte besitzen einen entlang der Schnittfläche verteilten Verlauf.^{2Die Schnittkraftverläufe in den entstandenen Schnittflächen heben sich gegenseitig auf.} Ohne diesen Verlauf im Detail zu kennen, können wir eine daraus resultierende Schnittkraft und ein resultierendes Schnittmoment bezüglich eines beliebigen Punktes S der Schnittflächen bilden. Nach der Einführung des Normaleneinheitsvektors e_n der Schnittfläche stellen wir die Gleichgewichtsbedingungen auf.

Die Kraftkomponenten in der Schnittfläche bezeichnen wir als

N = Normalkraft
Q = Querkraft
M = Biegemoment

Nachfolgend wollen wir ausschließlich schlanke Tragwerkselemente betrachten, bei denen eine Abmessung sehr viel größer ist als die restlichen (Balken, Rahmen).

Die Untersuchung der Schnittgrößen des Balkens beginnt mit einem Schnitt senkrecht zur Balkenachse.

Die Lage des Schnitts wird durch einen Parameter u entlang der Balkenachse festgelegt. Durch das Schneiden des Balkens erhalten wir ein linkes und rechtes Schnittufer. Die Richtung des Schnitts wird durch den Normaleneinheitsvektor $eu beschrieben, der senkrecht zum Schnittufer, also in Richtung der Balkenachse zeigt. Dabei wird jenes Schnittufer als positives Schnittufer_ bezeichnet, bei dem der Normalenvektor vom Balkeninneren nach außen gerichtet ist. positives Schnittufer Zur Ermittlung der Schnittgrößen des Balkens sind folgende Schritte notwendig:

• Ermittlung der Gelenkkräfte.
• Zerlegung des Balkens in Bereiche, in denen Belastungswechsel durch äußere Kräfte und Momente auftreten.
• Bestimmung der Schnittgrößengleichungen für die Einzelbereiche aus den Gleichgewichtsbedingungen.

Beispiel Ein Balken wird durch Axial- und Querkräfte belastet. Gesucht sind die Schnittgrößenverläufe.

Schnittgrößen:

-
N	N + A = 0 ⇒ N = −F	N + Ax − 2F = 0 ⇒ N = F	N + Ax − 2F + F = 0 ⇒ N = 0
Q	−Q + Ay = 0 ⇒ Q = 76·F	−Q + Ay − F = 0 ⇒ Q = 16·F	−Q + Ay − 2F = 0 ⇒ Q = −56·F
M	M − Ay·u = 0 ⇒ M = 76·F·u	M − Ay·u + F(u−2a) + 2F·a = 0 ⇒ M = 16·F·u	M − Ay·u + F(u−2a) + 2F·a − F·a + F(u−4a) = 0 ⇒ M = −56F·u+5F·a

Es besteht offensichtlich ein Zusammenhang zwischen der äußeren Belastung eines Balkens und den resultierenden Schnittgrößen. Für eine Untersuchung dieses Zusammenhangs wollen wir verallgemeinernd einen Balken beaufschlagt mit einer Streckenlast näher betrachten.

Zunächst schneiden wir ein kleines Balkenstück der Länge du frei. Wir approximieren die Streckenlast als Rechteck der Höhe q(u) und stellen dann die Gleichgewichtsbedingungen bezüglich des rechten Schnittufers auf.

Wir vernachlässigen getrost den Summanden mit du² und erhalten einen

Zusammenhang zwischen Streckenlast, Querkraft und Biegemoment

Q´= dQdu = − q(u)

M´= dMdu = Q´

mit

q(u) = Streckenlast

Q = Querkraft

M = Biegemoment

Daraus ergibt sich zudem die bekannte Abhängigkeit von Querkraft und Biegemoment gemäß Seite9_1.PNG. Die eigentlichen Schnittgrößen erhalten wir durch Integration unter Berücksichtigung von Randbedingungen.

Schnittgrößen:

Q(u) = −∫qdu + c₁

M(u) = ∫Qdu + c₂

Die nachfolgende Tabelle ist hilfreich zur qualitativen Skizzierung der Schnittgrößenverläufe

Belastung	N	Q	M
	Sprung	stetig	stetig
	stetig	Sprung	Knick
	stetig	stetig	Sprung
	Sprung	stetig	Sprung
	stetig	Gerade	quad. Parabel
	stetig	quad. Parabel	kub. Parabel

In Erweiterung des Einzelbalkens betrachten wir ein Tragwerk aus mehreren (schlanken) Bauteilen. Der Schnittgrößenverlauf hierbei ist erwartungsgemäß insofern einfach, daß zunächst die Lager- und Gelenkkräfte bestimmt und anschließend an den freigeschnittenen Einzelkörpern wiederum wie im vorangehenden Kapitel deren Schnittgrößenverläufe bestimmt werden. Hierfür ist folgende Gelenkübersicht hilfreich, die die Rand- und Übergangsbedingungen für Schnittgrößen zusammenstellt

Gelenk	Symbol	N	Q	M
Festgelenk, Einspannung		≠ 0	≠ 0	≠ 0
Drehgelenk, Festlager		≠ 0	≠ 0	= 0
Schubgelenk 1		= 0	≠ 0	≠ 0
Schubgelenk 2		≠ 0	= 0	≠ 0
Kurfengelenk, Loslager 1		= 0	≠ 0	= 0
Kurfengelenk, Loslager 2		≠ 0	= 0	= 0
freies Ende		= 0	= 0	= 0

Beispiel

Ein Tragwerk aus 2 Balken wird durch eine Kraft F und ein Moment M₀ belastet. Gesucht sind die Schnittgrößenverläufe.

Gleichgewichtsbedingungen: Körper 1:

Körper 2:

-	Körper 1	-
Bild
Q	−Q + A = 0 Q = −F	−Q + A = 0 Q = −F
M	M − A·x1 + MA = 0 M = −F·x1 + M0 + 2Fl	M − A·x1 + M0 + MA = 0 M = −F·x1 − M0 + M0 + 2Fl
-	Körper 2	-
Bild
Q	−Q − B = 0 Q = −F	−Q − B + C = 0 Q = F
M	M + F2·x2 = 0 M = −F·x2	M − B·x2 − C(x2 − l) = 0 M + F·x2 − 2F(x2 − l = 0) M = F·x2 − 2Fl

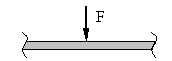
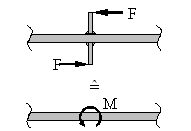
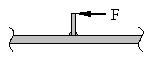
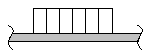
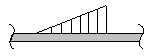
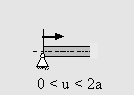Im Gegensatz zum Balken hat der Rahmen einen abgewinkelten Querschnittverlauf. Darüberhinaus können Verzweigungsstellen auftreten.

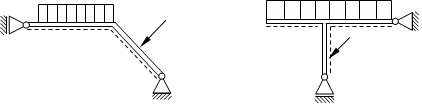
Damit auch bei abgewinkeltem Verlauf Verzweigungen eine eindeutige Schnittgrößenvereinbarung getroffen werden kann, wollen wir eine gestrichelte Bezugsfaser einführen, die jeweils die "Unterseite" eines Balkenelements kennzeichnet

Wir untersuchen nun die Schnittgrößen in einer Knickstelle und schneiden den Rahmen unmittelbar links und rechts davon frei.

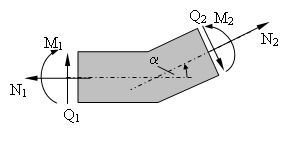
Die Transformationsmatrix der ebenen Rotation hilft uns, die Gleichgewichtsbedingungen für das Rahmenelement aufzustellen.

∑ F ≡  −N₁Q₁  +  cosα −sinαsinα cosα   N₂−Q₂  = 0

∑ F ≡  cosα sinα−sinα cosα   − N₁Q₁  +  N₂−Q₂  = 0

∑ M ≡ M₂ − M₁ = 0

Die Momente werden durch die Abwinkelung des Rahmens nicht beeinflußt. Die Normal- und Querkraft müssen über die entsprechenden Winkelfunktionen aufgeteilt werden, also gilt für die

Änderung der Schnittgrößen am abgewinkelten Rahmenelement

N₂ = N₁·cosα − Q₁·sinα

Q₂ = N₁·sinα − Q₁·cosα

M₂ = M₁

Für den praktisch bedeutsamen Fall eines 90°-Winkels erhalten wir

Vorgehensweise bei abgewinkeltem und verzweigtem Rahmen:

1. Festlegung einer Bezugsfaser (gestrichelte Linie) zur eindeutigen Orientierung der Schnittgrößen.
2. Zerlegung des Rahmens in gekennzeichnete Teile mit gerader Längsachse (Balken).
3. Bestimmung der Gelenkreaktionen mittels bekannter Methoden der Statik.
4. Abschnittsweise Bestimmung der Schnittgrößen und Berücksichtigung der Winkelfunktionen an Knicken im Rahmenverlauf.

Beispiel

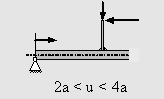
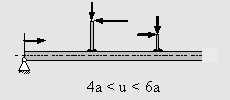
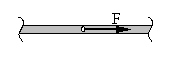
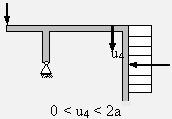
Ein abgewinkelter Rahmen mit Verzweigung wird durch die Kraft F belastet. Gesucht sind die Schnittgrößenverläufe.

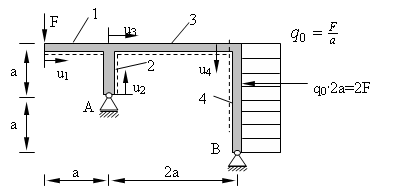
Gleichgewichtsbedingungen:

Auflagerkräfte:

-
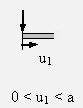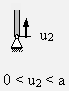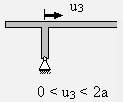
Q	−Q − F = 0 Q = F	−Q = 0 Q = 0	−Q − F + Ay = 0 Q = 32·F	−Q − q0·u4 = 0 Q = −Fa·u4
N	N = 0 N = 0	N + Ay = 0 N = −52·F	N = 0 N = 0	N = Q3 N = 32·F
M	M + F·u1 = 0 M = −F·u1	M = 0 M = 0	M + F(a + u3) − N1·u3 = 0 M = −F·A − 32·F·u3	M + M3 + q0·u4·u42 = 0 M = −F·a − 32·F·u3 + Fa·u42