Wir betrachten einen Körper, der zunächst von zwei Kräften belastet wird.

von links nach rechts 1), 2), 3);
Dabei wollen wir drei Fälle unterscheiden

• die Wirkungslinien der Kräfte schneiden sich
• die Kräfte sind parallel
• die Kräfte sind entgegengesetzt gleich groß

Im allgemeinen Fall des von 2 Kräften belasteten Körpers, dessen Kräftewirkungslinien sich in einem Punkt schneiden, lassen sich die Kräfte gemäß dem Verschiebungsaxiom in den Schnittpunkt verschieben

und anschließend nach dem Parallelogrammaxiom zu einer Resultierenden zusammenfassen.
Für gegebene Kraftangriffspunkte P₁ und P₂ findet man den Kraftangriffspunkt P_R der Resultierenden (Schnittpunkt) aus

also

Diese Gleichung ist allerdings nur gültig, solange F₁ und F₂ nicht parallel sind, also

ist.

Die Kräfte lassen sich aus dem Lageplan in den Kräfteplan überführen.

Kräfteplan

Sind die Kräfte nun mittels ihrer Beträge und relativen Winkellage gegeben (polare Koordinaten), so lassen sich in diesem Fall die geometrische Dreiecksbeziehung zur Ermittlung der Resultierenden heranziehen.

Greifen n Kräfte im gemeinsamen Schnittpunkt ihrer Wirkungslinien an, so ergibt sich die Resultierende als vektorielle Summe.

Lageplan                                  Kräfteplan

Die Resultierende des zentralen Kräftesystems ist die Summe aller beteiligten Kräfte.

F_R = n∑i=1·F_i

—-

Aufgabe

Geg.: F1=150 N F2=250 N α =30° Ges.: β	Eine in die Wand geschlagene Öse wird durch 2 Kräfte F1 und F2 belastet. Die Wirkungslinie der Kraft F1 besitzt den Winkel α zur Horizontalen. Mit welchem Winkel muß F2 angreifen, damit die Resultierende mit der Horizontalen zusammenfällt? Wie groß ist die resultierende Kraft?
I) graphische Lösung
	- Wahl des Kräftemaßstabs - Richtungsgerade von F1 mit 30° zur Horizontalen zeichnen - F1 der Länge 30 mm abtragen - Kreis um Spitze von F1 mit Radius=Länge von F2 (50 mm) - Resultierende FR vom Fußpunkt von F1 bis Schnttpunkt Kreis/Horizontale zeichnen - Winkel β ablesen: β =18° - Länge von FR ablesen: 74 mm 370 N
II) graphoanalytische Lösung*
	- qualitativen Kräfteplan zeichnen - Geometrische Grundaufgabe: 2 Seiten, 1 Winkel gegeben; Winkel gesucht
sin αsin β = F2F1 β = arcsin(F2FR·sinα) β = 17,46°	- Sinussatz anwenden - auflösen - einsetzen
F2R = F21 + F22 − 2F1F2cosγ mit γ = 180° − α − β	- Cosinussatz anwenden5alternativ ließe sich nochmals der Sinussatz anwenden
F2R = 22500 + 62500 − 2 · 150 · 250 · cos132,54 [N2] = 135721 · 105 [N2] FR^ = 368,4 N	- einsetzen
III) skalare Lösung*
Fx1 = F1cosα Fy1 = F1sinα Fx2 = F2cosβ Fy2 = − F2sinβ	- Zerlegung der Kräfte F1 und F2 in x- und y-Komponenten
FxR = F1cosα + F2cosβ FyR = F1sinα − F2sinβ mit FyR ≡ 0 ⇒ sinβ = F1/F2 sinα β = 17,46°	- Addition der Komponenten - Bedingung: vertikale Resultierende ≡ 0 liefert Winkel β
FR = FxR FR = 150cos30° + 250cos17,46° [N] FR = 368,4 N	- Resultierende als horizontale Komponente
F1 = 12·F1· √31  F2 = F2  cosβsinβ  FR = F1 + F2 FyR = 12·F1 + F2 sinβ ≡ 0 sinβ = 1·F12·F2 β = − 17,46° FR = 75 √31 + 250 cos−17.46°sin−17.46°  [N] FR =  368,40  N	- Kräfte F1 und F2 formulieren - Resultierende als Summe - y-Komponente der Vektorgleichung muß verschwinden6rein formal erhalten wir dieselbe Gleichung, indem wir fordern, daß das Produkt der Resultierenden mit dem y-Einheitsvektor verschwindet, d.h. FR ey = 0 - auflösen und einsetzen - Resultierende aus der Vektorsumme

Für die Wirkung einer Kraft auf einen starren Körper ist neben deren Größe und Richtung auch die Lage ihrer Wirkungslinie von Bedeutung.

von links nach rechts a), b), c);

Ist beispielsweise eine starre Scheibe im Punkt A derart gelagert, daß sie (in der Zeichenebene) um A drehbar ist, so hängt offensichtlich die Lage der Kraftwirkungslinie relativ zum Drehpunkt ursächlich mit der Drehbewegung (Drehrichtung) der Scheibe zusammen. In den drei dargestellten Fällen wird jeweils ein Körper mit Kraft F belastet. Im Fall a) wird eine Drehbewegung im mathematisch positiven Sinn, im Fall c) eine mathematisch negative Drehung erzeugt. Im Fall b) ruft die Kraft gar keine Drehung hervor. Das Bestreben einer Kraft, einen starren Körper um einen Punkt zu drehen, ist umso größer, je größer die Kraft und je länger der Abstand dieser Kraft zum Drehpunkt (Hebelarm) ist. Als Maß für die Drehwirkung einer im Punkt P angreifenden Kraft F dient das auf einen beliebigen Punkt A bezogene Moment^{7auch statisches Moment oder Drehmoment} M_A. Dieses Moment M_A ist demnach proportional zur Größe der Kraft und dem Abstand d ihrer Wirkungslinie zum Drehpunkt A. Wir definieren also

Das Moment ist eine skalare Größe^{8 gilt nur bei ebenen Kräftesystemen; bei räumlichen Problemstellungen ist das Moment ein Vektor} und hat die Einheit [Nm]. Darüberhinaus besitzt das Moment eine Drehrichtung, die durch positives Vorzeichen bei mathematisch positivem Drehsinn und durch negatives Vorzeichen bei mathematisch negativem Drehsinn gekennzeichnet wird.

Betrachten wir die x- und y-Komponenten der Kraft F und des Vektors d vom Drehpunkt A zum Angriffspunkt P, so ergibt sich das Moment dieser Kraft aus diesen Komponenten in skalarer Schreibweise zu

Dies ist allerdings identisch mit der

vektoriellen Schreibweise des Moments^{9im Raum gilt M_A=d F}

M_A = F·d^{^}

mit d=P-A

Die vektorielle Form der Momentengleichung hat den Vorteil, daß man sich dabei nicht um das Vorzeichen kümmern muß. Dieses ergibt sich automatisch aus der Richtungsinformation des Abstandsvektors d. Hierbei ist zu beachten, daß der Abstandsvektor immer vom Drehpunkt zum Kraftangriffspunkt zeigt. Da die Kraft entlang ihrer Wirkungslinie verschoben werden kann, genügt zur Festlegung von P ein beliebiger Punkt auf dieser Wirkungslinie. Greifen an einem Körper n Kräfte an, so ergibt sich das resultierende Gesamtmoment aus der Summe aller Einzelmomente dieser Kräfte um einen Punkt A, also

resultierendes Gesamtmoment mehrere Kräfte

M_res = n∑i=1 M_i = n∑i=1 F_i·d^{^}_i

Nachdem wir zwei Kräfte gemäß dem Verschiebungsaxiom in den Schnittpunkt ihrer Wirkungslinien verschoben und diese dann nach dem Parallelogrammaxiom zu einer Resultierenden zusammengefaßt haben^{10siehe Kapitel: Die Resultierende des zentralen Kräftesystems} , können wir diesen Vorgang mit dieser Resultierenden und einer weiteren Kraft jeweils wiederholen. Auf diese Weise gelangen wir schließlich graphisch zur Lage der Resultierenden einer ebenen Kräftegruppe.

Wir wollen hier Größe und Lage der resultierenden Kraft analytisch ermitteln.

Hinsichtlich der Drehwirkung muß die Summe aller Einzelmomente äquivalent dem Moment der Resultierenden sein. Daraus ermitteln wir die Lage der Wirkungslinie der Resultierenden über die Momentengleichung bezüglich des Punktes A, also

Nehmen wir weiterhin an, daß d_Res senkrecht auf der Wirkungslinie der Resultierenden F_Res steht und bezeichnen den Einheitsvektor dieser Wirkungslinie mit e_Res.

mit

Das resultierende Moment formulieren wir damit als

und erhalten so die

Lage der Resultierenden der ebenen Kräftegruppe

d_Res = −M_ResF2Res · F^{^}_Res

oder in skalarer Komponentenschreibweise

x_dRes = M_ResF2Res · F_yRes

y_dRes = −M_ResF2Res · F_xRes

Diese Gleichungen sind nur dann anwendbar, wenn die resultierende Kraft F_Res nicht verschwindet (F_Res ≠ 0).

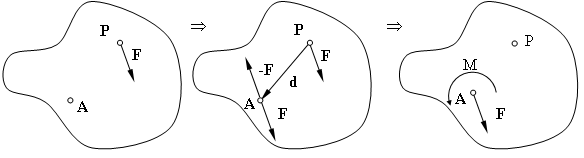
Parallele Einzelkräfte

Wir wollen folgenden Spezialfall der Belastung eines Einzelkörpers untersuchen:

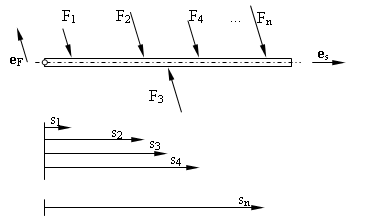
Dabei besitzen alle auf den Körper wirkenden Kräfte parallele Wirkungslinien. Zur Lösung eines solchen Problems böte sich ein leistungsfähiges graphisches Verfahren an - die Konstruktion nach der Seileckmethode^{11Die Seileckmethode führt eine zweifache graphische Integration durch} . Die Bedeutung des Seilecks geht grundsätzlich über die Anwendung auf rein statische Probleme hinaus. Wir wollen uns hier allerdings auf die vektoriell-analytische Methode beschränken.
Dazu führen wir im ersten Schritt eine körperfeste Wirkungslinie parallel zu allen Kraftvektoren ein und bezeichnen deren Einheitsvektor mit e_F.

Eine Kraft F_i dieser Kräftegruppe läßt sich dann als

schreiben. Vereinbaren wir weiterhin eine körperfeste Achse mit dem Einheitsvektor e_s. Damit erzeugt die Kraft F_i in einem Punkt A auf dieser Achse ein Moment

Summieren wir über alle Einzelkräfte, erhalten wir als Resultierende

Über die Äquivalenz der Momente

erhalten wir

Resultierende der parallelen Kräftegruppe

F_Res = n∑i=1 · F_i

s_Res = n∑i=1 · F_i·s1F_Res

Streckenlast

Verallgemeinern wir nun in einem nächsten Schritt anhand dieser Überlegung die Belastung des Körpers auf eine kontinuierlich verteilte Streckenlast q(s) mit der Dimension Kraft/Länge (N/m).

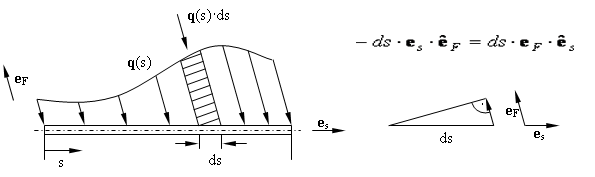
Ein herausgeschnittenes Stück dieser Streckenlast der infinitesimalen Länge ds kann dann durch die Einzelkraft

ersetzt werden.
Im Grenzübergang erhalten wir bei einer Anwendung der Gleichung für die Resultierende der parallelen Kräftegruppe mit einer Ersetzung der Summen durch Integrale die

Resultierende der Streckenlast

F_Res = ∫q(s)ds

s_Res = ∫q(s) · s · dsF_Res

Die Streckenlast hat bei der Betrachtung von Tragwerken eine große praktische Bedeutung. So lassen sich damit beispielsweise

• Belastungen eines Trägers durch Eigengewicht
• Schneelasten auf Dächern
• Windkräfte auf Krananlagen oder Schornsteine
• Druckbelastung auf die Wandung eines Flüssigkeitsbehälters

erfassen.^{12die Annahme einer Streckenlast ist nur für schlanke Bauteile zulässig. Andernfalls sind Flächenlasten einzusetzen}

Beispiel

Mit dem Parameter s, der vom linken Balkenrand startet, wird die Last mittels der Geradengleichung

beschrieben. Die resultierende Kraft ergibt sich damit durch Integration

Den Angriffsort s_Res der Kraft ermitteln wir aus

Eine Einzellast

vom linken Balkenrand hat also die gleiche statische Wirkung wie die gegebene Dreieckslast.

Wir wollen nun einen Körper mit zwei Kräften belasten, die gleich groß und entgegengesetzt gerichtet sind.

Die resultierende Kraft

verschwindet. Sodann bilden wir die Momentensumme (resultierendes Moment) um einen beliebigen Pol A.

Moment des Kräftepaares

M = d^{^}₁₂ · F

mit

d^{^}₁₂ = P₂ − P₁

und P₁, P₂ als beliebige Punkte auf den Kraftwirkungslinien

Damit haben wir das resultierende Moment eines Kräftepaares ermittelt. Das Ergebnis ist dabei in mehrfacher Hinsicht bemerkenswert:

• Das resultierende Moment des Kräftepaares ist unabhängig von der Lage des Pols.
• Ein Kräftepaar und damit ein Moment läßt sich bei gleichbleibender Wirkung beliebig in der Wirkungsebene parallel verschieben (weder Kräftesumme, noch Momentensumme ändert sich).
• Ein Kräftepaar d^{^}₁ · F₁ kann durch ein anderes Kräftepaar d^{^}₂ · F₂ bei gleicher Wirkung auf den Körper ersetzt werden, wenn M = d^{^}₁ · F₁ = d^{^}₂ · F₂ gilt.
• Mehrere Momente lassen sich zu einem resultierenden Moment zusammensetzen (Addition).

Ein Kräftepaar und ein zugehöriges Moment sind in ihrer Wirkung auf einen Körper identisch. Nachfolgend wird bevorzugt der Begriff

auf einen Körper wirkendes Moment

benutzt.
Das Moment gemäß M = d^{^} · F wird null, wenn

• die Kraft F null ist
• der Vektor d der Nullvektor 0 oder parallel zu F ist.

Betrachten wir den Sonderfall, daß der Vektor d orthogonal zum Vektor der Kraft F liegt, wobei e_F der Einheitsvektor von F sei.

Dies führt auf die skalare Form der Gleichung des Kräftepaars

M = d · F

mit d = Abstand zwischen den Kraftwirkungslinien und F = Betrag einer Einzelkraft

Die Richtungsinformation des Moments ist hierbei allerdings verlorengegangen und aus den Richtungen der Einzelkräfte zueinander zu beschaffen.

Auf einen Körper wirke im Punkt P eine Kraft F.

Uns interessiert allerdings eine Belastung im Punkt A, die der Kraft F in Punkt P äquivalent ist. Dazu tragen wir die Kraft F zusätzlich im Punkt A an und kompensieren diese gleichzeitig mit der entgegengesetzt gleich großen Kraft %u2013F ebenfalls im Punkt A, um das Gleichgewichtsaxiom zu erfüllen.

Dadurch erhalten wir ein Kräftepaar

und eine Kraft F im gewünschten Punkt A.

Die Parallelverschiebung einer Kraft F entlang des Verschiebungsvektors d muß mit dem Hinzufügen eines Moments M = d^{^}·F einhergehen, damit die Wirkung auf den betreffenden Körper unverändert ist.^{13Das hinzuzufügende Moment heißt Versatzmoment.}

Umgekehrt läßt sich diese Methode zur Momentenkompensation einsetzen. Wirkt in einem Körperpunkt A eine Kraft F und ein Moment M, so gibt es mindestens einen Verschiebungsvektor d, entlang dem die Kraft verschoben werden kann, damit

das entstehende Versatzmoment genauso groß wie das aktuell wirkende Moment ist und entgegengesetzte Drehrichtung besitzt.

Wenn sich alle an einen ebenen Körper angreifenden Kräfte und Momente gegenseitig aufheben, dann ist dieser im Gleichgewicht. Die sogenannten Gleichgewichtsbedingungen lauten:

∑F = 0

∑M = 0

Diese Gleichgewichtsbetrachtung spielt eine zentrale Rolle bei der Behandlung statischer Problemstellungen und besagt:

Ein Körper verharrt im Zustand der gleichförmigen, geradlinigen Bewegung, wenn er nicht durch einwirkende Kräfte gezwungen wird, diesen zu ändern.^{14Beharrungsprinzip, Trägheitssatz von Newton}

Die bisher zu ermittelnde resultierende Kraft eines ebenen Kräftesystems muß nunmehr bei der vorliegenden Gleichgewichtsbetrachtung verschwinden. Das dazu gehörige Krafteck muß sich dabei grundsätzlich schließen. Ebenso muß das resultierende Moment um einen beliebigen Punkt Null ergeben.^{15Die graphische Analogie dazu lautet: das Seileck muß geschlossen sein.}

Für ein hier betrachtetes ebenes Kräftesystem erhalten wir somit aus den Gleichgewichtsbedingungen maximal drei skalare Gleichungen^{16Diese drei Gleichungen korrespondieren mit den drei Freiheitsgraden eines Körpers in der Ebene}, mit welchen sich maximal drei unbekannte Kraft- oder Momentengrößen ermitteln lassen. Jede dieser Größen kann eine Kraftkomponente (x- oder y-Komponente), eine Kraftgröße (Moment oder Bezug einer Kraft) oder die Richtung einer Kraft (Einheitsvektor) sein.

Statt der beiden skalaren Kräftegleichungen und der Momentenbeziehung ist es allerdings auch möglich, mit einer Kraft und zwei Momentenbedingungen zu arbeiten, oder gar das Momentengleichgewicht bezüglich dreier unterschiedlicher Punkte aufzustellen.

Dabei lauten die Bedingungen im Klartext:

• Die Pole A und B dürfen nicht auf einer Geraden liegen, die senkrecht zur Richtung steht, in der die Kräftebedingung gebildet ist.
• Die Pole A, B und C dreier Momentenbedingungen dürfen nicht auf einer gemeinsamen Geraden liegen.

Für den Sonderfall des zentralen ebenen Kräftesystems gehen die Wirkungslinien aller Kräfte durch den gemeinsamen Schnittpunkt P. Dabei ist die auf P bezogene Momentensumme in jedem Fall null. Verschwindet darüberhinaus die resultierende Kraft, so liegt ein zentrales Gleichgewichtssystem vor. In diesem Fall genügt als

Gleichgewichtsbedingung für das zentrale Kräftesystem

∑F = 0

Für den Sonderfall des parallelen ebenen Kräftesystems läßt sich die Kräftesumme

als Summe aller skalaren Kraftgrößen bezogen auf die gemeinsame Kraftrichtung e_F formulieren. Damit gilt die

Gleichgewichtsbedingung für das parallele Kräftesystem

∑F = 0

∑M = 0

Wegen der großen praktischen Bedeutung eines durch drei Kräfte belasteten Körpers sei dieses Ergebnis nochmals hervorgehoben.

Wird ein ebener Körper ausschließlich durch drei Kräfte belastet, so schneiden sich deren Wirkungslinien in einem gemeinsamen Punkt.