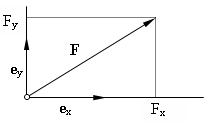
Einheitsvektor
Jeder Vektor u läßt sich durch einen skalaren Faktor u und einen normierten vektoriellen Anteil eu ausdrücken
Multiplikation von Vektor und Skalar
c·u
c·u ist ein Vektor, der zu u parallel und gleich- oder entgegengesetzt gerichtet ist, je nachdem ob c positiv oder negativ ist.
(1.3)v = c·
u =
u·c;
vxVy = c·
uxuy =
cuxcuy
Insbesondere der Faktor %u20131 führt auf einen entgegengesetzt gerichteten gleich großen Vektor, den negativen Vektor.
(1.4)u·(−1) = (−1)·
u = −
u
Addition und Subtraktion von Vektoren
Vektoren werden addiert, indem ihre Komponenten addiert werden. Die Reihenfolge der Summanden ist vertauschbar.
(1.5)v =
u1 +
u2 =
u2 +
u1 (Kommutativgesetz)
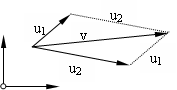
(1.6) vxvy =
u1x + u2xu1y + u2y
Entsprechend werden Vektoren subtrahiert, indem ein negativer Vektor addiert wird.
u1 = v + (−u2) = v − u2
(1.7) u1xu1y =
vx − u2xvy − u2y
Betrag eines Vektors
Der Betrag eines Vektors entspricht dessen Länge. Wir erhalten ihn aus
(1.8)u = √u
2 = √(u
2x + u
2y)
Der Einheitsvektor eu zu einem gegebenem Vektor errechnet sich aus
(1.9)eu =
uu =
u√(u2x + u2y)
Skalarprodukt
Unter dem skalaren oder inneren Produkt zweier Vektoren u und v verstehen wir die Summe der Produkte ihrer Komponenten
(1.10)s =
u·
v =
uxuy ·
vxvy = u
x·v
x + u
y·v
y
Darüberhinaus gilt das Kommutativgesetz
und das Distributivgesetz
Insbesondere gilt für die Multiplikation eines Vektors mit sich selbst
Das skalare Produkt zweier senkrecht aufeinander stehender Vektoren ist 0.
u·v = 0 mit u ⊥ v
Weiterhin ergibt die Multiplikation eines Vektors mit einem Einheitsvektor einen Zahlenwert
,
der der Länge der Projektion von u auf e entspricht.
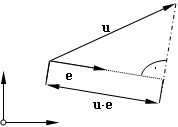
Der projizierte Vektor entsteht damit aus
Es gilt nicht das Assoziativgesetz, d.h.
Orthogonaloperator
Bei einer Beschränkung auf ebene Vektoren findet das Vektorprodukt oder Kreuzprodukt nur eingeschränkte Verwendung
,da es einen Vektor erzeugt, der senkrecht auf der betrachteten Ebene steht. Stattdessen wird der sogenannte Orthogonaloperator ^ eingeführt,

der einen zu u um 90° mathematisch positiv gedrehten (orthogonalen)
u^ Vektor erzeugt.
In Verbindung mit dem Orthogonaloperator gelten folgende weitere Rechenregeln:
| u^^ = −u | 2 fache Drehung |
| (u + v)^ = u^+v^ | gedrehter Summenvektor |
| u^·v^ = u·v | Produkt gedrehter Vektoren |
| u^·v = −u·v^ | Vertauschungsregel |
| u·u^ = 0 | Punkt senkrechter Vektoren |
| (u´)^ = (u^)´ | Differentiation |
Insbesondere gilt für die Einheitsvektoren des kartesischen Koordinatensystems
ex = −e^y
ey = −e^x
Winkel zwischen 2 Vektoren
Wie bereits erwähnt, lassen sich Vektoren über ihre Längen und Winkel zur x-Achse beschreiben.
u = u cosαsinα ; v = v cosβsinβ
Das Skalarprodukt führt dabei auf
(1.19)u·
v = uv(cosα cosβ + sinα sinβ)
und unter Berücksichtigung der Additionstheoreme der Trigonometrie
(1.20)u·
v = u·v cos(β − α) = u·v cosγ
mit dem zwischen den Vektoren eingeschlossenen Winkel %uF067. Andererseits liefert
(1.21)uv^ = uv(−cosα sinβ + sinα cosβ)
und das entsprechende Additionstheorem
(1.22)u^v = uv sin(β − α) = u·v sinγ
Damit ergeben sich folgende Winkelfunktionen:
für den von u nach v gerichteten Winkel %uF067 gilt:
sinγ = u^·vuv
tanγ = u^·vu·v
Vektorgleichungen
Beim Umgang mit Vektorgleichungen bieten sich weitgehend dieselben Möglichkeiten wie bei algebraischen Gleichungen. Als Beispiel betrachten wir den geschlossenenen Vektorzug dreier Vektoren.
Entsprechend der Anzahl der Komponenten läßt sich die Vektorgleichung in zwei skalare Gleichungen aufspalten (Gleichungssystem).
yu + yv + yw = 0
Eine Vektorgleichung läßt sich nach einer Unbekannten auflösen.
Sie kann quadriert werden
(1.27)u
2 = v
2 + 2
vw + w
2 (vektorieller Cosinussatz)
oder mit einem Skalar oder Vektor multipliziert werden,
wobei die Multiplikation mit einem Vektor die Vektorgleichung in eine algebraische Gleichung überführt.
Durch Multiplikation mit dem Einheitsvektor läßt sich die skalare Größe isolieren.
Schließlich kann ein Summand u durch den Faktor aus der Gleichung entfernt werden.
Die Vektorgleichung kann durch eine skalare Größe dividiert werden.
Die Division durch einen Vektor ist dagegen grundsätzlich nicht erlaubt.