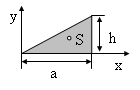
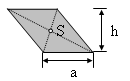
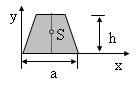
Innerhalb von geometrieverarbeitenden Softwaresystemen (CAD) werden Flächenkonturen häufig durch geschlossene Polygonzüge angegeben. Als Polygonzug wird eine - hier ebene - Kurve bezeichnet, deren Stützpunkte durch Strecken linear verbunden sind.
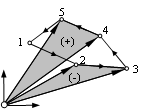
Die Stützpunkte werden derart fortlaufend gekennzeichnet, daß die Kurve ihre eingeschlossene Fläche in mathematisch positivem Sinn umfährt. Damit liegt das Innere des Polygonzugs grundsätzlich links einer Kante.
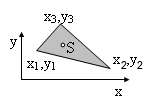
Die Dreiecksfläche , die eine Kante des Polygonzugs (Punkt P
i und P
i+1) mit dem Koordinatenursprung aufspannt, gehorcht der Beziehung (s.
Beispiel)
Ai = P^i · Pi+1
und ist positiv, wenn die Kante ein "positives Moment" um den Koordinatenursprung besitzt (d.h. in mathematisch positive Richtung dreht), ansonsten negativ.
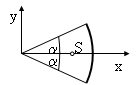
Für die Bestimmung des Schwerpunktes dieser Fläche nutzen wir die geometrische Eigenschaft des Dreiecks, daß der Schwerpunkt auf der Seitenhalbierenden liegt und diese Strecken im Verhältnis 2:1 teilt.
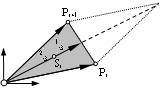
Den Vektor der Seitenhalbierenden erhalten wir mittels
12(Pi + P<i+1)
und die Lage des Schwerpunkts
Si = 13(Pi + P>i+1)
Damit können wir den Schwerpunkt des Polygonzugs über die Summe aller Teilflächen ermitteln.
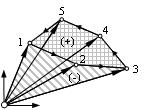
Wegen des Vorzeichens der Dreiecksflächen erhalten wir als Ergebnis den
Schwerpunkt eines geschlossenen Polygonzugs
S = 13·n∑i=1·(Pi+Pi+1) · (P^i+Pi+1)n∑i=1· P^i+Pi+1
für
i = n setze i+1 = 1