Die bisherige Betrachtung eines isolierten einzelnen Körpers ist eine wichtige Grundvoraussetzung für einen Übergang hin zur Untersuchung eines Systems von mehreren starren Körpern^{17engl. systems of rigid bodies}.
Uns interessiert dabei primär die Übertragung von Kräften zwischen diesen Körpern. Damit zwei Körper gemäß dem Reaktionsaxiom gegenseitig Kräfte übertragen können, müssen diese Körper irgendwie untereinander verbunden sein. Dies wird genauer formuliert durch:

Zwischen zwei Körpern ist eine Bindung^{18engl. constraint} notwendig, damit diese Körper Kräfte übertragen können.

und

Eine Bindung zwischen zwei Körpern beschränkt diese in ihren Bewegungsmöglichkeiten zueinander.

Hierzu ist nicht unbedingt ein körperlicher Kontakt notwendig, da ja auch Fern- oder Volumenkräfte eine Art von Bindung darstellen.

Nachfolgend wollen wir topologische Merkmale von Systemen starrer Körper untersuchen:

• unterschiedliche Bindungen (Gelenke, Lager)
• unterschiedliche Geometrie und Eigenschaften der betrachteten Körper (Seil, Rahmen)
• unterschiedliche Belastungsarten (Stab, Balken) Beispiel eines Tragwerks
  
  Im Zentrum der statischen Betrachtung stehen Systeme von Körpern, die insgesamt vollständig in ihrer Beweglichkeit eingeschränkt sind^{19oder zumindest als momentan unbeweglich angenommen werden} und lediglich Kräfte übertragen. Ein solches System nennen wir Tragwerk.

Damit ein einzelner Körper, der sich innerhalb eines Tragwerks befindet, statisch berechnet werden kann, sind alle auf ihn wirkenden -einschließlich der durch Bindungen übertragenen- Kräfte zu berücksichtigen.
Dazu wird der Körper zunächst gedanklich vollständig aus seinen Bindungen heraus gelöst.^{20Freischneiden, Freimachen eines Körpers} Dadurch werden die (inneren) Reaktionskräfte in den Bindungen zu äquivalenten äußeren Kräften.

Lösen der Bindungen eines Tragwerks
Als hilfreiche Vorstellung dient dabei die Überlegung, den Körper oder u.U. nur Teile davon durch einen gedachten Schnitt vollständig aus seiner Umgebung herauszulösen. Zweck dieser Vorgehensweise ist die Feststellung, welche Kräfte angrenzende Körper auf das betrachtete Tragwerksteil ausüben.^{21Die vom Tragwerksteil auf die umgebenden Körper gemäß dem Reaktionsprinzip übertragenen Kräfte interessieren hier dagegen nicht.} Freigeschnittene Körper mit ihren Bindungskräften
eim Lösen eines Körpers aus seinen Bindungen sind einige wichtige Regeln zu beachten.

Freischneiden eines Körpers:

• Vollständigkeit: Ein Körper darf nur ganz oder gar nicht freigeschnitten werden. Wichtig ist dabei, daß alle Reaktionskräfte erfaßt werden.
• Bindungskräfte: In den gelösten Bindungen werden die von den Umgebungselementen auf den Körper wirkenden Kräfte und Momente aufgetragen.
• Konsistenz: Werden mehrere Körper gleichzeitig freigeschnitten, müssen in den gelösten Bindungen zwischen diesen Körpern die Kräfte und Momente jeweils entgegengesetzt gerichtet angetragen werden.

Bestimmte Belastungsarten und Bindungstypen geben bereits Aufschluß über Richtung und/oder Richtungssinn der Bindungskräfte und -momente in den gelösten Bindungen. Nachfolgend werden spezielle Tragwerkselemente und Gelenke hinsichtlich dieser Merkmale untersucht.

Ein Tragwerk besteht aus einzelnen Bauelementen (Körpern), den sogenannten Tragwerkselementen.

Gestell

Das Gestell^{22engl. ground, auch Umgebung, Erde, Fundament} bildet das Fundament eines Tragwerks. Es nimmt lediglich Kräfte und Momente auf, im Sinne der Erzeugung von Reaktionskräften, und überträgt keine Kräfte und Momente im Sinne derer Weiterleitung.
Das Gestell wird üblicherweise nicht vollständig dargestellt, sondern lediglich fragmentarisch im Bereich der Gelenke.

Als Besonderheit des Gestellkörpers gilt dessen Freiheitsgrad f_Gestell = 0.
Eine gebräuchliche Darstellungsweise bedient sich dabei vorzugsweise einer Schraffur. Die Bedeutung dieser Symbolik wird nachfolgend während der Behandlung der Gelenke näher untersucht.

Stab

Wenn an einen Körper nur zwei Kräfte angreifen, dann müssen diese gemäß dem Gleichgewichtsaxiom gleich groß und entgegengesetzt gerichtet auf derselben Wirkungslinie liegen, damit der Körper im Gleichgewicht ist.
In diesem Fall bezeichnet man den Körper als Stab und die Kraftwirkungslinie als Stabachse.
Sehr häufig sind die Kraftangriffspunkte als reibungsfreie Drehgelenke ausgebildet.

Je nachdem, ob der Stab eine Zug- oder Druckbelastung erfährt, kann er darüberhinaus als Zugstab oder Druckstab bezeichnet werden.          Zugstab        Druckstab
Auf einen Stab wirkt grundsätzlich keine Querbelastung und kein Moment. Ein Stab, der drehgelenkig zwischen einem anderen Körper und dem Fundament gelagert ist, wird auch als Pendelstütze bezeichnet.
Treffen wir in einem Tragwerk auf einen Stab, so gilt:

Ein Stab hat eine bekannte Kraftwirkungslinie, der Richtungssinn und die Größe der wirkenden Kräfte ist zunächst nicht bekannt.

Seil

Ein Tragwerkselement, das lediglich Zugkräfte aufnehmen kann und für andere Belastungen weich ist, wird als Seil bezeichnet

Seile ( In Kombination mit Rollen )

Wenn ein Seil an zwei definierten Punkten befestigt ist, entspricht es einem Zugstab.
Sehr häufig treten Seile in Tragwerken kombiniert mit Rollen auf.

Dabei wird bei einer reibungsfrei gelagerten Umlenkrolle die Seilkraft lediglich umgelenkt. Für ein Seil innerhalb eines Tragwerks läßt sich folgende Aussage treffen:

Sowohl die Wirkungslinie, als auch der Richtungssinn der Kräfte in einem Seil sind bekannt, unbekannt ist dagegen deren Größe.

Für eine nähere Betrachtung soll ein wichtiger allgemeiner Fall untersucht werden.

Die Gleichgewichtsbedingung hinsichtlich Kräfte und Momente ergibt hierbei

mit

und

bzw. bei momentenfreier Lagerung, d.h. reibungsfrei gelagerter, nicht angetriebener Rolle

mit

und schließlich bei reibungsfrei gelagerter Rolle und einfacher Umlenkung des Seils (r1=r2)

mit

Balken, Träger

Für ein geradliniges (nicht gekrümmtes oder abgewinkeltes) Tragwerkselement,

                  Balken             Träger

das durch Kräfte quer zu seiner Achse oder durch Momente belastet wird, benutzen wir die Bezeichnung Balken oder Träger. Dabei werden horizontal liegende Elemente eher Balken und vertikal ausgerichtete Elemente bevorzugt Träger genannt.

Bei Balken oder Trägern kann über die Wirkungslinie, die Richtung und Größe der angreifenden Kräfte keine allgemeingültige Aussage getroffen werden.

Rahmen, Bogen

Ein gekrümmter Balken heißt Bogen und ein abgewinkelter Balken wird als Rahmen bezeichnet.

Darüberhinaus gelten die gleichen Aussagen wie für Balken und Träger.

Scheibe

Nicht schlanke Tragwerkselement sind sogenannte Scheiben.

Scheiben Die Belastung einer Scheibe liegt grundsätzlich in ihrer Ebene^{23eine senkrecht zu ihrer Ebene belastete Scheibe heißt Platte.} .

Über die Kräfte, die auf eine Scheibe wirken, lassen sich keine allgemeingültigen Aussagen treffen.

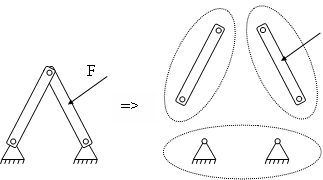
Lager und Gelenke^{24engl.: bearings and joints} Die Körper eines Tragwerks, wie Stäbe, Balken, Rahmen, etc., sind untereinander durch Gelenke verbunden.

Ein Gelenk stellt eine Bindung zwischen zwei Körpern dar, beschränkt die relative Bewegungsmöglichkeit in bestimmten Richtungen und erzeugt Kräfte (Gelenkreaktionen) in eben diesen Richtungen.
Zwischen der Anzahl der Gelenkreaktionen r und dem relativen Freiheitsgrad f eines ebenen Gelenks besteht der Zusammenhang r=3−f

Eine Klassifikation von Gelenken kann entweder nach Art und Anzahl der relativen Gelenkfreiheitsgrade oder umgekehrt nach Art und Anzahl der Gelenkreaktionen erfolgen.

Die Kräfte im Gelenk werden auch als innere Kräfte bezeichnet und gehorchen dem Reaktionsaxiom (actio=reactio).

Bindungen zwischen zwei Körpern werden allgemein als Gelenk bezeichnet, die besondere Bindung zwischen einem Körper und dem Gestell häufig als Lager oder Auflager.

Drehgelenk

Eine Verbindung zwischen zwei Körpern, die lediglich eine relative Drehung um den Gelenkpunkt zuläßt, wird Drehgelenk genannt.

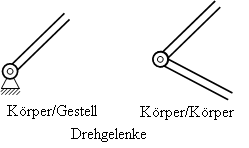
Ein Drehgelenk hat als relative Bewegungsmöglichkeit die Rotation um den Drehpunkt und damit den

Freiheitsgrad f_Dreh = 1

Andererseits verhindert das Gelenk eine relative Verschiebung und kann so Kräfte in Richtung der x- und y-Achse übertragen. Die Anzahl der Gelenkreaktionen beträgt

Reaktionen r_Dreh = 2

Mit dem Drehgelenk läßt sich lediglich eine Kraft übertragen. Die freie Drehbeweglichkeit läßt keine Momentenübertragung zu. D.h.

Die Richtung der Kraft im Drehgelenk ist nicht spezifiziert.

Schubgelenk

Das Schubgelenk läßt nur eine Verschiebung entlang einer gemeinsamen Schubachse zu.

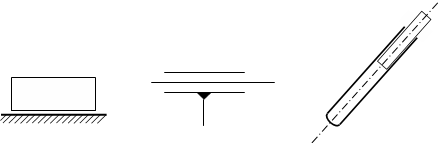
Aus dieser relativen Bewegungsmöglichkeit ergibt sich ein

Freiheitsgrad f_schub = 1

Gleichzeitig verhindert das Schubgelenk eine Verschiebung senkrecht zur Schubachse sowie eine Drehung und kann daher eine Kraft und ein Moment aufnehmen.

Reaktionen r_Schub = 2

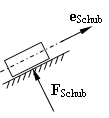
Wegen F_Schub ⊥ e_Schub gilt

Kurvengelenk, Loslager

Sogenannte Kurvengelenke sind durch die Führung eines Punktes des Körpers entlang einer Kurve des jeweils anderen Körpers gekennzeichnet.

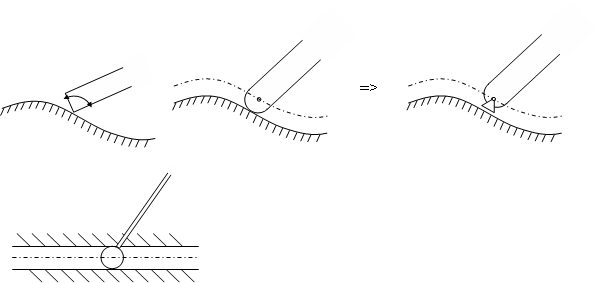
Dieses Kurvengelenk läßt sowohl eine Verschiebung entlang der Kurve, als auch eine Drehung um den Verschiebungspunkt zu.
Diese Bewegungsmöglichkeiten entsprechen einem

Freiheitsgrad f_Kurve = 2

Entsprechend der Bindung kann das Kurvengelenk lediglich eine Kraft senkrecht zur Kurventangente analog zum Schubgelenk weiterleiten.

Reaktionen r_Kurve = 1

Diese spezielle Form des Kurvengelenks (

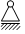
) wird in der Statik als Loslager bezeichnet.

starre Verbindung, Einspannung

Die feste Verbindung zweier Körper verhindert jegliche Relativbewegung,

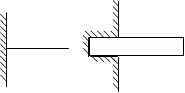
also gilt

Freiheitsgrad f_star = 0

Folglich kann über eine starre Verbindung eine Kraft unbekannter Richtung und Größe und ein Moment weitergeleitet werden.

Reaktionen r_star = 3

Stab als Gelenk

Anstatt einen Stab als Körper aufzufassen, können wir ihn auch als spezielles Gelenk interpretieren.

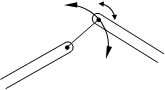
Betrachten wir in diesem Sinne zwei Körper, die durch einen Stab verbunden sind. Denken wir uns dann einen Körper festgehalten (Relativbewegung), so läßt sich der andere um diesen Körper auf einer Kreisbahn (Radius=Stablänge) und gleichzeitig um seinen Stabanlenkpunkt drehen.
Damit hat ein Stab als Gelenk den

Freiheitsgrad f_star = 2

und verhindert eine Bewegung in Richtung der Stabachse. Also gilt

Reaktionen r_star = 1

Der Stab kann also Kräfte entlang seiner Stabachse aufnehmen. Aufgrund seiner Drehbeweglichkeit wird kein Moment übertragen.

Seil als Gelenk====Analog zum Stab können wir auch das Seil als besonderes Gelenk auffassen.

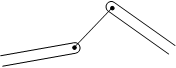
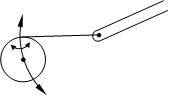
Wenn das Seil an zwei Körperpunkten befestigt ist, verhält es sich wie ein Stab. Dabei ist die Besonderheit zu beachten, daß es nur Zugkräfte überträgt. Ist der zweite Körper eine Rolle, auf die das Seil aufläuft, lassen sich die Beweglichkeiten folgendermaßen interpretieren:

1. Drehung der Rolle um den Anlenkpunkt des Seils am ersten Körper.
2. Abwälzen der Rolle auf der Seilgeraden. Dies sind ebenfalls zwei Freiheitsgrade. 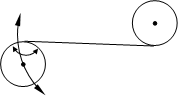Als dritte Möglichkeit untersuchen wir das Seil, das von einer Rolle abläuft und auf eine weitere aufläuft.
   Beim Festhalten einer Rolle ergeben sich folgende Beweglichkeiten der anderen Rolle:
3. Drehbewegung der betrachteten Rolle um die festgehaltene Rolle^{25Tatsächlich bewegt sich die Rolle hier nicht auf einer Kreisbahn, sondern auf einer sogenannten Evolvente.} .
4. Wälzen der Rollen auf der Seilgeraden.

Freiheitsgrad f_Seil = 2

besitzt. Die Bindung (Verhindern einer Bewegung) erfolgt in Richtung der Seilgeraden, also gilt

Reaktionen r_Seil = 1

mit der Besonderheit, daß das Seil starr ist bei Zug und weich bei Druck und damit nur Zugkräfte überträgt.
Das Seil als Gelenk ist nicht imstande Momente zu übertragen. Damit ist aber gemeint, daß das Seil kein Moment zwischen den beteiligten Körpern überträgt. Die Reaktionskraft des Seils erzeugt allerdings grundsätzlich ein Moment auf die Seilrolle bezüglich des Rollenmittelpunkts.

Nachdem bisher die relativen Freiheitsgrade und die Reaktionen der einzelnen Gelenke untersucht wurden, wollen wir jetzt den Freiheitsgrad eines Systems starrer Körper bestimmen.
Wie bereits erwähnt, besitzt der ebene starre Körper den Freiheitsgrad f_Körper = 3. Die Betrachtung eines Systems von n solchen Körpern, die zunächst untereinander keine Bindung besitzen, führt somit auf den Gesamtfreiheitsgrad

Zusätzlich wollen wir von den betrachteten Körpern genau einen als Gestell mit dem Freiheitsgrad null definieren. Dadurch korrigiert sich die vorstehende Beziehung entsprechend zu^{26Im allgemeinen Fall mehrerer Gestellkörper ist korrekterweise anzusetzen fSystem=3(n-nGestell)Mehrere Gestellkörper werden jedoch üblicherweise in der Statik und Kinematik als ein einzelner Körper betrachtet.}

In einem weiteren Schritt werden die Körper durch Gelenke verbunden. Dabei raubt jedes Gelenk Freiheitsgrade entsprechend der Anzahl Gelenkreaktionen, also

(4.9)f_ges = 3(n − 1) − g∑i=1·r_i

bzw.

f_ges = 3(n − 1 + g) + g∑i=1·f_i

mit

n = Anzahl der Körper

g = Anzahl der Gelenke

r_i = Anzahl Reaktionen des i−ten Gelenks

f_i = Anzahl Freiheitsgrade des i−ten Gelenks

Die Bestimmung des Gesamtfreiheitsgrades eines Systems starrer Körper ist eine Voraussetzung für die statische Rechnung. Dabei gilt:

f_ges > 0; Mechanismus, statisch unterbestimmt

f_ges = 0; Tragwerk, statisch bestimmt

f_ges < 0; Tragwerk, statisch überbestimmt

Die Kräfte innerhalb eines Systems starrer Körper lassen sich nur unter der Voraussetzung f_ges = 0 ermitteln.
Liegt ein Mechanismus mit f_ges > 0 vor, so kann dieser durch Hinzufügen oder Verändern geeigneter Gelenke in ein statisch bestimmtes Tragwerk überführt werden.^{27 Dies ist nur zulässig, wenn keiner der Körper zum Zeitpunkt der Betrachtung eine Beschleunigung erfährt. Andernfalls müssen Methoden der Kinetostatik eingesetzt werden.}
Treffen wir dagegen auf ein statisch überbestimmtes Tragwerk, so muß die Annahme der Starrkörpereigenschaft aufgegeben und mit den Hilfsmitteln der Elastostatik gearbeitet werden.
Eine wichtige Eigenschaft der Bestimmungsgleichung des Gesamtfreiheitsgrades sei nachfolgend an einem Beispiel verdeutlicht.

Beispiel: wirksamer Freiheitsgrad

Die beiden Tragwerke a) und b) besitzen jeweils n=5 Körper und g=6 Drehgelenke und damit den Gesamtfreiheitsgrad f_ges = 0.
Während das linke Tragwerk (a) entsprechend seinem Freiheitsgrad unbeweglich ist, weist die rechte Tragwerksvariante im Einklang mit unserer Erfahrung und Anschauung eine Beweglichkeit (Instabilität) auf. Eine derartige Beweglichkeit tritt nur bei speziellen geometrischen Besonderheiten auf (hier Parallelität).
Wegen der grundsätzlichen Möglichkeit, daß solch ein Sachverhalt -erkennbar oder nicht- vorliegt, gilt:

Das Ergebnis der Bestimmungsgleichung für den Gesamtfreiheitsgrad f_ges = 0 ist eine notwendige aber nicht hinreichende Bedingung für die Unbeweglichkeit und statische Berechenbarkeit eines Tragwerks.^{28Es handelt sich dabei ja um eine reine Abzählbedingung, die keinerlei Information über die Gelenkanordnung beinhaltet.}

Gelegentlich werden bei einem Tragwerk mit einem Freiheitsgrad >0 (Mechanismus) zusätzlich unbekannte gleichgewichtshaltende Kräfte eingeführt. Diese sind äquivalent zu entsprechenden unbekannten Lagerreaktionen und erfüllen ebenfalls die Bedingung der statischen Bestimmtheit.

Sind mehr als zwei Körper in einem Punkt miteinander verbunden, so sind dort soviele Gelenke zu berücksichtigen, daß definitionsgemäß jedes Gelenk genau zwei Körper verbindet. In solchen Fällen macht es u.U. Sinn, statt der beteiligten Körper das Gelenk freizuschneiden. Auch hierbei muß die Gleichgewichtsbedingung erfüllt sein.

Tragwerke bestehen aus mehreren Körpern und müssen hinsichtlich der Tragfähigkeit ihrer Gelenkverbindungen untersucht werden^{30Eine Untersuchung der Tragfähigkeit der Körper selbst erfolgt mittels der Elastostatik.}. Zur konstruktiven Gestaltung der Gelenke werden häufig Normteile wie Schraubverbindungen, Linearführungen, Wälzlager, etc. verwendet, deren Hersteller maximale Belastungen angeben. Als Berechnungsingenieure eines Tragwerks müssen wir in diesem Zusammenhang sicherstellen, daß die von uns dimensionierten Verbindungen unterhalb ihrer Bauteilbelastungsgrenze beansprucht werden. Zu diesem Zweck werden wir die auftretenden Kräfte und Momente in allen Gelenken ermitteln^{31zumindest in den Gelenken, die uns aufgrund unserer Erfahrung als die kritischen erscheinen}

allgemeine analytische Lösung

In einer allgemeinen Vorgehensweise wird ein Tragwerk zunächst auf seine statische Bestimmtheit überprüft und im nächsten Schritt werden alle Körper freigemacht. Dabei erhalten wir entsprechend der Gesamtzahl Freiheitsgrade 3(n-1) Bestimmungsgleichungen für die gesuchten Gelenkreaktionen.
Beispiel:

n=3 => f=6 : F_A, F_B, F_C
Körper 1:

Körper 2:

Damit haben wir 6 Gleichungen für 6 Unbekannte vorliegen.

Eine willkommene Eigenschaft der verwendeten Gleichgewichtsbedingungen ist die Tatsache, daß Kräfte und Momente als Unbekannte stets linear in den Gleichungen auftreten. Die zu lösenden Gleichungen bilden somit ein lineares Gleichungssystem.

mit der Koeffizientenmatrix A, dem unbekannten Vektor x und dem Vektor r der rechten Seite.

Beispiel (Fortsetzung):

Körper 1:	∑Fx ≡ FAx − FCx = 0 ∑Fy ≡ FAy − FCy = 0 ∑MA ≡ −FC·r^AC = 0
Körper 2:	∑Fx ≡ FBx + FCx + Fx = 0 ∑Fy ≡ FBy + FCy + Fy = 0 ∑MB ≡ FC·r^BC + FC·r^BD = 0

Wir bringen alle bekannten Größen auf die rechte Seite, nutzen

und erhalten das lineare Gleichungssystem

das üblicherweise in Matrix-/Vektorschreibweise formuliert wird

Es ist typisch für Probleme der Statik, daß die Koeffizientenmatrix A ausschließlich durch Geometriegrößen gebildet wird, der Unbekanntenvektor x die gesuchten Kraftgrößen darstellt und die rechte Seite r die gegebenen, sog. eingeprägten Kräfte und Momente beinhaltet. Derart formalisierte Gleichungsstrukturen lassen sich besonders einfach in einer höheren Programmiersprache codieren. Dazu wird bevorzugt das Gauss´sche Eliminationsverfahren in einer seiner Varianten herangezogen. Die Lösung solcher Probleme läßt sich dann mit Hilfe eines Rechners durchführen.

statisch bestimmte Tragwerksteile

Bei der Bestimmung der Gelenkreaktionen muß nicht immer jeder einzelne Körper freigeschnitten werden. Unter Umständen ist es hilfreich, ein oder mehrere Tragwerksteile, die ihrerseits aus mehreren Körpern bestehen, als Ganzes freizuschneiden und quasi als einzelnen Körper aufzufassen.

Dies ist allerdings nur zulässig, wenn der Freiheitsgrad dieses Tragwerkteils analog zum einzelnen Körper

beträgt.

Superpositionsprinzip

Die Eigenschaft statischer Problemstellungen, lineare Funktionen der gesuchten Kräftgrößen zu liefern, erlaubt erfreulicherweise folgenden Berechnungstrick:
Wenn ein Tragwerk durch mehrere Kräfte belastet ist, kann es nacheinander für jede dieser Einzellasten gerechnet werden. Die Summe dieser einzeln gefundenen Gelenkreaktionen ergeben die

aus der Gesamtbelastung resultierenden Gelenkkräfte.
Am Beispiel des durch die Kräfte F₁ und F₂ belasteten Zweischlags vereinfacht sich dadurch die Ermittlung der Auflagerkräfte, da sich durch die Beschränkung auf jeweils eine Kraft einer der beiden Körper als Stab erweist. Die Tragwerke sind dadurch einfacher zu behandeln.
Um die Richtigkeit dieser Vorgehensweise zu zeigen, sei das Gleichungssystem des Zweischlags mittels

formuliert. Die Aufteilung in Einzelkräfte ergibt

und deren Addition

Wegen der Eigenschaft von xi und ri lineare Funktionen von F₁ und F₂ zu sein, gilt

Ein durch mehrere Kräfte und/oder Momente belastetes Tragwerk kann mittels Überlagerung der durch die einzelnen Lastfälle gewonnenen Gelenkreaktionen statisch berechnet werden. Diese Vorgehensweise nennt man Superpositionsprinzip.

Hinweis:
Das Superpositionsprinzip leistet nur dann erleichternde Hilfestellung, wenn die unterschiedlichen Kräfte und Momente an verschiedenen Körpern angreifen. Andernfalls ist es sinnvoller, die Resultierende der Kräfte oder Momente zu bilden und damit weiterzurechnen.

Ein Tragwerk, das ausschließlich aus Stäben besteht, wird als Fachwerk bezeichnet. Die Tatsache, daß diese Stäbe ausschließlich auf Zug oder Druck belastet werden, zusammen mit der Eigenschaft des Stabes, eine hohe Widerstandsfähigkeit gegen eine reine Längsbelastung aufzuweisen, führt insgesamt zu einer sehr material- und damit gewichtssparenden Konstruktion.

Die Gelenkpunkte eines Fachwerks werden Knoten genannt.

Das ideale Fachwerk\\

• wird ausschließlich in den Knoten belastet
• besitzt reibungsfreie Drehgelenke

Diese idealisierenden Annahmen treffen in der Praxis nur annähernd zu. Die Stäbe werden allgemein mittels starrer Knotenbleche verschraubt oder verschweißt. Eine Querbelastung der Stäbe durch ihr Eigengewicht, Windkräfte, Schneelasten, etc. bilden Streckenlasten entlang der Stabachsen, die im Widerspruch zur Definition des rein längsbelasteten Stabs stehen.
Trotzdem erweisen sich die Berechnungsergebnisse anhand eines idealisierten Fachwerks als gute Annäherung der realen Verhältnisse.^{32 Nicht vernachlässigbare Streckenlasten werden dabei häufig je zur Hälfte als Last auf die benachbarten Knoten verteilt.}

Freiheitsgrad des Fachwerks

Zur Ermittlung des Freiheitsgrades eines ebenen Fachwerks betrachten wir zunächst die k Knoten als ausdehnungslose Körper mit je einem Freiheitsgrad von f_Knoten=2 in der Ebene. Zwischen den Knoten bestehen Bindungen durch s Stäbe, die die relative Bewegung zweier benachbarter Knoten in Stabrichtung beschränken (r_Stab=1). Damit erhalten wir den

Freiheitsgrad des Fachwerks

f_Fachwerk = 2 k − s− r_Gestell

mit s = Anzahl der Stäbe
k = Anzahl der Knoten
r_Gestell = Summe aller Gestellreaktionen

Die Forderung f_Fachwerk=0 führt zur

Bedingung für das statisch bestimmte ebene Fachwerk^{33für das statisch bestimmte räumliche Fachwerk gilt s = 3k - rGestell}

s = 2k − r_Gestell

Beispiel:

Berechnungsverfahren

Die Ermittlung der Tragfähigkeit eines Fachwerks ist gleichbedeutend mit der Bestimmung aller Stabkräfte. Das bisher praktizierte Verfahren des Freischneidens aller Körper -hier Stäbe- erweist sich bei einem Fachwerk wenig vorteilhaft. Stattdessen haben sich bis heute verschiedene Verfahren bewährt:

• rechnerische Verfahren
  1. Knotenschnittverfahren (Knotenpunktverfahren)
  2. Rittersches Schnittverfahren
  3. Finite Elemente Analyse (FEA)
• graphische Verfahren
  1. Cremona-Plan
  2. Hennebergsches Stabtauschverfahren Im Hinblick auf die rechnergestützte Fachwerkanalyse eignen sich vor allem das Knotenschnittverfahren und die FEA. Zur Nachrechnung einiger weniger Stabkräfte per Hand erweist sich das Rittersche Schnittverfahren als recht nützlich. Die graphischen Verfahren haben heute nur noch untergeordnete Bedeutung.

Nullstäbe

In einem statisch bestimmten Fachwerk sind häufig Stäbe zu finden, die bei einer gegebenen Belastung keine Kraft übertragen. Diese Stäbe werden als Nullstäbe^{34auch Blindstäbe} bezeichnet.
Vor einer Berechnung der Stabkräfte ist es zweckmäßig, solche Nullstäbe zu lokalisieren und entsprechend zu kennzeichnen. Hierbei helfen folgende

Regeln zur Erkennung von Nullstäben:

1. Zwei nicht gleichgerichtete Stäbe an einem unbelasteten Knoten^{35d.h. durch keine äußere Kraft belasteter Knoten} sind Nullstäbe.
2. Wenn zwei nicht gleichgerichtete Stäbe an einem belasteten Knoten zusammentreffen und die Kraft F in Richtung eines dieser Stäbe verläuft, dann ist der andere Stab ein Nullstab.
3. Besitzen von drei an einem Knoten angeschlossenen Stäben zwei dieselbe Richtung, dann ist der dritte ein Nullstab.

Beispiel:

Nullstab	wg. Regel
4	2
5	3
9	3
10	1
11	1

Bei diesem Verfahren werden statt der Stäbe die Knoten freigeschnitten. Dies führt auf eine deutlich reduzierte Zahl von Gleichgewichtsbedingungen. Für jeden Knoten liegt dabei ein zentrales Kräftesystem vor und wir erhalten dazu die 2 Gleichungen des Kräftegleichgewichts. Beispiel:

	Annahme: Knoten grundsätzlich durch Zugstäbe belastet Für das dargestellte Fachwerk sind alle Stabkräfte zu bestimmen
Überprüfung:	Knotenschnittverfahren: statische Bestimmtheit? s = 2k - 3 => 9 = 9
∑ Fx ≡ Ax + F = 0 ∑ Fy ≡ Ay + By −3F = 0 ∑ MA ≡ −2Fa + Fa − 3Fa + By · 2a = 0 ⇒ Ax = −F; Ay = F; By = 2F	Gestellreaktionen?
∑ Fx ≡ Ax + S1 + 12 √2 S2 = 0 ∑ Fy ≡ Ay − 12 √2 S2 = 0 ⇒ S1 = 0; S2 = √2 F	Knoten A:
∑ Fx ≡ − S1 + 12 √2 S4 = 0 ∑ Fy ≡ − S3 − 12 √2 S4 = 0 ⇒ S3 = 0; S4 = 0	Knoten C:
∑ Fx ≡ − 12 √2 S2 + 12 √2 S6 + S5 = 0 ∑ Fy ≡ S3 + 12 √2 S2 − 12 √2 S6 − 2F = 0 ⇒ S5 = 2F; S6 = − √2 F	Knoten D:
∑ Fx ≡ F − 12 √2 S4 + 12 √2 S8 − S5 = 0 ∑ Fy ≡ − S7 + 12 √2 S4 − 12 √2 S8 = 0 ⇒ S7 = −F; S8 = √2 F	Knoten E:
∑ Fx ≡ − S9 − 12 √2 S8 = 0 ∑ Fy ≡ 12 √2 S8 − F = 0 ⇒ S9 = − F	Knoten G:
∑ Fx = 0 ∑ Fy = 0 ⇒	Knoten B: Alles bekannte Kräfte! Kann zur Kontrolle gerechnet werden.

Sind nur einige Stabkräfte eines Fachwerks zu bestimmen, so bietet sich vorteilhaft das Verfahren nach Ritter an. Dazu wird das Fachwerk durch einen Schnitt in zwei Teile zerlegt. Hierbei unterliegt der Schnittverlauf allerdings gewissen Einschränkungen:

Ritterscher Schnitt durch

• 3 Stäbe
  1. die nicht parallel sind
  2. die nicht alle am selben Knoten angeschlossen sind
• Stab und Knoten, wobei der Stab nicht an diesen Knoten anschließt.

Dadurch erhalten wir jeweils 2 Teilfachwerke, die beide für sich im Gleichgewicht sein müssen. Die Besonderheit der Schnittführung resultiert damit in 3 unbekannten (Stab- oder Konten-) Kräften, für die dann drei Gleichgewichtsbedingungen aufgestellt werden können. Wirken auf das gewählte Teilfachwerk zusätzlich Gestellreaktionen, so sind diese Lagerkräfte im voraus am Gesamtsystem zu ermitteln.

Beispeil:

Wie ändert sich die Stabkraft in 1, wenn Stab 2 durch 2* ersetzt wird?

Ritter-Schnitt durch 1-2-3