Die Kräfte, die auf einen Massenpunkt während der Kreisbewegung wirken, korrespondieren mit den entsprechenden Beschleunigungen.

Mit Bezug auf die d'Alembertschen Trägheitskräfte erhalten wir in tangentialer Richtung die der Tangentialbeschleunigung entgegengesetzte Tangentialkraft

sowie in radialer Richtung die der Zentripetalbeschleunigung entgegengerichtete Zentrifugalkraft (Fliehkraft).

Ein Punkt auf einer gleichmäßig rotierenden Kreisscheibe besitzt die tangentiale Geschwindigkeit

Der Betrag der Geschwindigkeit v_t wächst linear mit zunehmendem Radius r. Somit erfährt ein Punkt, der sich während dieser Drehung auf einer (scheibenfesten) Geraden in radialer Richtung bewegt, offensichtlich eine Beschleunigung – er begibt sich aus einer Region mit geringer in eine solche mit höherer Tangentialgeschwindigkeit. Die daraus resultierende Coriolisbeschleunigung weist bei zunehmendem Radius in Drehrichtung und bei abnehmendem r entgegengesetzt dazu. Der Betrag der Coriolisbeschleunigung gehorcht der Beziehung

wie wir sie bei der allgemeinen Punktbewegung hergeleitet haben.

Ist der Punkt dagegen frei auf der Scheibe beweglich, so wird er bei seiner Bewegung einer gekrümmte Bahn (bezüglich der Scheibe) folgen.

[Quelle: Wikipedia]

Auch hier korrespondieren die Kräfte auf den Massenpunkt mit den entsprechenden Beschleunigungen gemäß dem dynamischen Grundgesetz.

Als d'Alembertschen Trägheitskräfte erhalten wir in tangentialer Richtung die der Coriolisbeschleunigung entgegengesetzt gerichtete Corioliskraft

Zusätzlich wirkt noch die Zentrifugalkraft in radialer Richtung

Aufgabe:

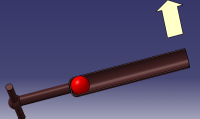
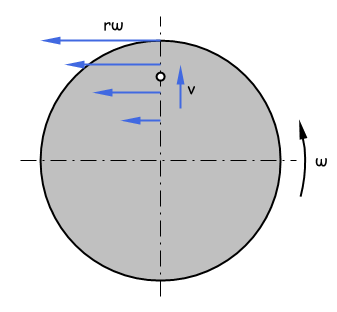
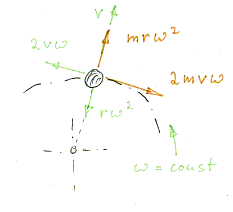
Eine Kugel liegt in einem Rohr, welches rotiert. (Die Erdbeschleunigung wird hierbei vernachlässigt.)

Gegeben:

• r₀ = 10 cm
• r₁ = 50 cm
• n = 5 s⁻¹
• m = 50g
  
  

Gesucht:

1. Der Winkel Φ, nach dem die Kugel das Rohr verlässt.
2. Die Geschwindigkeit (Betrag und Richtung) mit welcher die Kugel das Rohr verlässt
3. Das Moment M, welches an der Drehachse des Rohres notwendig ist um diese Bewegung hervorzurufen
   
   
   

Lösung:

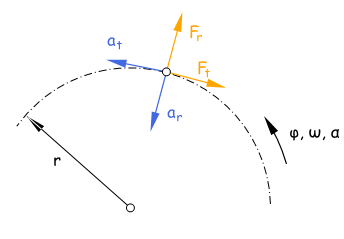
Es gilt:

Gleichgewichtsbedingung in radialer Richtung:

Mit Gleichung (1) folgt daraus die lineare, homogene Differentialgleichung

Diese wir gelöst durch eine Funktion der Form r(t)=A·e^{ω t}:

• r(t)=A·e^{ω t}
• r^·(t)=A·ω·e^{ω t}
• r^··(t)=A·ω²·e^{ω t}
  

Überprüfung durch Einsetzen:
A·ω²·e^{ω t} − A·e^{ω t}·φ^·2=0 wird mit φ^·≡ω² zu
A·ω²·e^{ω t}=A·ω²·e^{ω t} -> Gleichung erfüllt!

Mit der Anfangsbedingung r(t₀=0)=r₀ ergibt sich für A:
r(0)=A·e^{ω 0}=r₀
⇒ A=r₀

Die Bewegungsgleichungen in radialer Richtung sind somit:

• r(t)=r₀·e^{ω t}
• v(t)=r₀·ω·e^{ω t}
• a(t)=r₀·ω²·e^{ω t}