Vom bisher betrachteten einzelnen Massenpunkt verallgemeinern wir nun auf ein System von n Massenpunkten.

Der Massenpunkt i besitzt den Freiheitsgrad f_i=2 in der Ebene und f_i=3 im Raum. Lassen wir nun starre Bindungen r_ij zwischen zwei Massen i und j zu, reduziert sich der

Gesamtfreiheitsgrad

(7.1)f = D·n − k

mit

D = Dimension (Raum: 3, Ebene: 2)

n = Anzahl Massenpunkte

k = Anzahl starrer Bindungen

Diese Beziehung entspricht der Gleichung zur Bestimmung des Freiheitsgrades von Fachwerken (ohne Lager).

Ein System von 3 Massen, von denen jede mit den jeweils anderen verbunden ist, führt auf den Freiheitsgrad f_2D = 3 bzw. f_3D = 6. Dies stimmt mit dem Freiheitsgrad eines Körpers in der Ebene und im Raum überein – wie wir später sehen werden.

Die momentane Lage eines Massenpunkts i sei bezüglich eines globalen, nicht bewegten Koordinatensystems (Inertialsystem) durch den Ortsvektor r_i beschrieben.

Hieraus erhalten wir die Lage des Massenmittelpunkts (Gesamtschwerpunkt) des Massenpunktsystems.

Massenmittelpunkt

(7.2)r_S = 1m · n∑i=1 m_i·r_i

mit

Gesamtmasse m = n∑i=1 m_i

Die auf eine Masse m_i wirkenden Kräfte bilden ein zentrales Kräftesystem. Alle äusseren Kräfte, einschliesslich der Lagerreaktionen, lassen sich zu einer Resultierenden F_i zusammenfassen.

Die inneren Kräfte in den – nicht notwendigerweise starren – Bindungen treten stets paarweise auf (actio = reactio)

Die Gleichgewichtsbedingung einer Masse i einschliesslich der d'Alembertschen Trägheitskraft lautet

Bei der Summation über alle Kräfte auf alle Massenpunkte verschwinden wegen der paarweisen Gegenläufigkeit alle inneren Kräfte und es resultiert unter Berücksichtigung der zweifachen Ableitung von 7.2 nach der Zeit der

Schwerpunktsatz

n∑i=1F_i − n∑i=1m_i ·r••i = 0

bzw.

(7.3)F_S − m·a_S = 0

Der Gesamtschwerpunkt eines Massenpunktesystems bewegt sich so, als würden alle äusseren Kräfte an ihm angreifen und als wäre die gesamte Masse in ihm konzentriert.

Der Impuls eines einzelnen Massenpunkts ist

Aus dieser Beziehung haben wir bereits das dynamische Grundgesetz für zeitlich invariante Massen durch Ableitung gewonnen.

Den Gesamtimpuls eines Systems von Massenpunkten erhalten wir unmittelbar durch Differenzieren von Gl. 7.2.

Der Gesamtimpuls vieler Massenpunkte

(7.4)p = m·v_S = n∑i=1 m_i·v_i

ist gleich dem Produkt aus Gesamtmasse und Geschwindigkeit des Massenmittelpunkts.

Der Schwerpunktsatz 7.3 folgt offensichtlich aus der Ableitung von Gl. 7.4 nach der Zeit. Diese Tatsache bezeichnen wir als

Impulssatz

(7.5)p^• = F_S

Die zeitliche Änderung des Impulses entspricht der im Massenmittelpunkt wirkenden resultierenden Kraft.

Gebräuchlicher ist der Impulssatz jedoch in seiner integrierten Form

Impulssatz in integrierter Form

(7.6)p₁ − p₀ = m·v₁ − m·v₀ = t₁∫t₀F dt

Das Integral einer von Aussen wirkenden Kraft über der Zeit wird als Kraftstoß bezeichnet.

Der Impulssatz kann in solchen Fällen vorteilhaft angewendet werden, in denen eine äußere Kraft eine Masse über eine gewisse Zeit belastet und dadurch eine Änderung der Geschwindigkeit dieser Masse bewirkt.

Eine weitere – praktisch wichtige – Anwendung des Impulssatzes ergibt sich aus dem Sonderfall, in dem gar keine äußere Kraft existiert (F = 0). Hierbei gilt der

Impulserhaltungssatz

(7.7)p₀ = p₁ = const

Wirken keine äußeren Kräfte, dann bleibt der Gesamtimpuls eines Systems von Massenpunkten konstant.

Dieser Sachverhalt lässt sich vorteilhaft bei der Behandlung von Stoßvorgängen ausnutzen.

Anmerkung: Eine eingehende Behandlung solcher Stoßvorgänge erfolgt gegenwärtig nicht.

Wir wollen nun die Drehwirkung – das "Moment" – des Impulses einer einzelnen Masse näher untersuchen. Hierbei beschränken wir uns zunächst auf ebene Problemstellungen.

Die Lage einer Masse m sei durch den Ortsvektor r bezüglich eines festgelegten Koordinatenursprungs gegeben. Wir formulieren den Impuls dieser Masse

unter Verwendung von Polarkoordinaten gemäß Gl 2.2 als

Die Multiplikation dieser Beziehung mit r·e_φ führt über

auf das Impulsmoment bzw. den

Drehimpuls

(7.8)L = m·r²·φ^•

Ein Vergleich mit dem Flächensatz offenbart interessanterweise eine Proportionalität des Drehimpulses mit der Flächengeschwindigkeit (Gl. 2.12).

Den Zusammenhang zum Moment M stellen wir über das dynamische Grundgesetz

her, indem wir Gl 2.3 verwenden und auch hier beidseitig mit r·e_φ multiplizieren.

Auf der linken Seite steht das Moment M und auf der rechten Seite überlebt nur der zirkuläre Anteil der Beschleunigung wegen e_r ⊥ e_φ

Ein Vergleich mit dem Impulsmoment 7.8 führt zur Erkenntnis, dass hier dessen zeitliche Ableitung vorliegt.

Momentensatz

(7.9)M = dLdt = m·r²·φ^•• + 2 m·r·r^•·φ^•

Das Moment einer am Massenpunkt angreifenden Kraft F bezüglich eines Punktes O ist gleich der zeitlichen Ableitung des Drehimpulses bezüglich desselben Punktes.

Für ein System von n Massenpunkten erhalten wir dessen Gesamtimpuls aus der Summe aller Einzelimpulse gemäß Gl. 7.8.

Das Gesamtmoment resultiert aus der zeitlichen Ableitung des Gesamtimpulses

bzw. aus der Summe aller Einzelmomente nach Gl. 7.9.

Im allgemeinen räumlichen Fall ist der Drehimpuls ebenso wie das Moment ein Vektor. Er gehorcht der Beziehung:

Drehimpulsvektor

(7.10)L = r × p = r × m·v

Der Momentenvektor ergibt sich aus der zeitlichen Ableitung des Drehimpulsvektors

Momentenvektor

(7.11)M = dLdt = n∑i=1r_i × F_i

bzw. aus der Summe der Einzelmomente aller Kräfte auf die Massenpunkte.

In Analogie zum Impulserhaltungssatz gilt für den Fall, daß kein äußeres Moment wirkt, der

Drehimpulserhaltungssatz

L₀ = L₁ = const

Für ebene Problemstellungen können wir also schreiben:

Für den – in der Praxis wichtigen – Sonderfall der Kreisbewegung führen wir die Bezeichnungen

ein und erhalten die Beziehungen

Impulssatz

(7.10)L = Θ·ω

Momentensatz

(7.11)M = Θ·α

für die ebene Drehbewegung eines Massenpunktes.

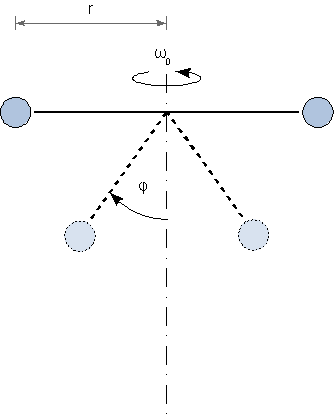Eine Eiskunstläuferin wird im Training mit Hanteln ausgestattet. Diese werden horizontal mit gestreckten Armen vom Körper weggehalten, während die Sportlerin eine Anfangsdrehbewegung mit konstanter Winkelgeschwindigkeit ω₀ für ihre Pirouette erreicht.

Um nun ihre Winkelgeschwindigkeit zu erhöhen, legt die Kunstläuferin mit Unterstützung der Schwerkraft ihre Arme nach unten an den Körper an.

Welchen Winkel φ müssen die Arme mit der Körperachse einschliessen, wenn die Winkelgeschwindigkeit verdoppelt werden soll?

Annahme: Das Massenträgheitsmoment des eigenen Körpers gegenüber den Hanteln soll hier ebenso vernachlässigt werden, wie die Reibungseinflüsse "Schlittschuhe auf Eis".

Nach Erreichen der Anfangsdrehzahl wirkt kein äußeres Moment mehr. Daher gilt zwischen den beiden betrachteten Armstellungen die Drehimpulserhaltung

Also

Wir erhalten unmittelbar

und daraus