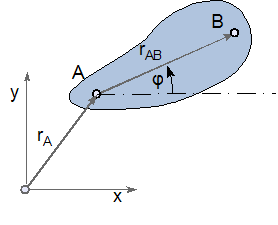
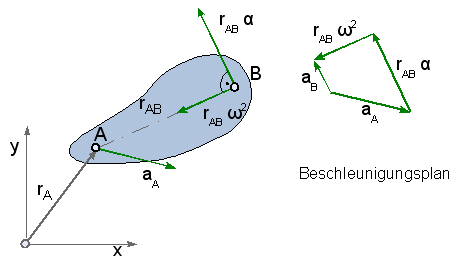
Nachdem der Nachweis gelungen ist, dass sich die allgemeine Starrkörperbewegung als überlagerte Translation und Rotation darstellen lässt, wollen wir nun überprüfen, ob sich der Geschwindigkeitszustand einer ebenen Bewegung als reine Drehbewegung um einen ausgezeichneten Punkt – den Momentanpol – auffassen läßt.
Als einzigen Anhaltspunkt auf der Suche nach diesem Momentanpol haben wir seine Eigenschaft, momentan geschwindigkeitslos zu sein.
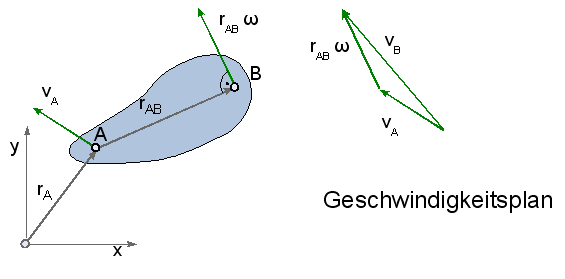
Es seien die Geschwindigkeiten zweier Körperpunkte vA und vB gegeben.
(a)vM =
vA + ω ·
r^AM =
0
(b)vM =
vB + ω ·
r^BM =
0
Die Lage des Momentanpols M relativ zu den Punkten A und B führt zum geschlossenen Vektorzug des Dreiecks <ABM>
bzw – wenn wir dieses um 90° drehen – auf
r^AB + r^BM − r^AM = 0
Die Verwendung der Gleichungen (a) und (b) ergibt
r^AB − 1ω(vB − vA) = 0
Wir multiplizieren diese Gleichung skalar mit r^AB und erhalten für die Winkelgeschwindigkeit den Ausdruck
(8.7)ω =
(vB − vA) · r^ABr2AB
Gleichung 7.8 lautete in Komponentenschreibweise
(8.7a)ω =
xAB (vAy − vAy) − yAB (vBx − vAx)x2AB + y2AB
und vereinfacht sich für den praktisch bedeutsamen Sonderfall, in dem die Geschwindigkeiten vA und vB gleichgerichtet sind und senkrecht auf dem Richtungsvektor rAB stehen, zu
Die Lage des Momentanpols lässt sich nunmehr Gleichung (c) entnehmen
rAM = rAB + rBM
und führt unter Verwendung von (a) auf
bzw. in Komponentenschreibweise
yAM = yAB − vBxω
Für den oben erwähnten Sonderfall der gleichgerichteten Geschwindigkeitsvektoren ergibt sich aus der x–Komponenten Gleichung von (8.9a) und (8.8) die Gleichung der Lage des Momentanpols als
wie sie sich alternativ auch aus der Anwendung des Strahlensatzes ergeben hätte.