Analog zu der Normalspannung σ , die senkrecht zur Schnittebene steht, definieren wir eine Schubspannung τ tangential zur Schnittebene.

Normalspannung/-verformung - Schubspannung/-verformung

Durch die Schubbeanspruchung erfährt der Körper als Formänderung die sog. Gleitung mit dem Gleitwinkel γ.

Wie der Zugversuch zeigt auch der Scherversuch einen linearen Zusammenhang zwischen Schubspannung τ und Gleitwinkel γ im elastischen Bereich.

Hooke´sches Gesetz für Schubbeanspruchung

τ = G · γ

mit

τ = Schubspannung

γ = Gleitwinkel

G= Schubmodul

Entsprechend dem Elastizitätsmodul E ist auch der Schubmodul G eine Materialkonstante. Zwischen diesen beiden und der Querkontraktionszahl ν besteht ein

Zusammenhang der Werkstoffkonstante

E = 2G(1−ν)

mit

E= Elastizitätsmodul

G= Schubmodul

ν= Querkontraktionszahl

         Scherstift         Schweißnaht
Greifen zwei gleich große Kräfte mit parallelen, nahe beieinander liegenden Wirkungslinien an einen Körper an, so wird der dazwischen liegende Querschnitt auf Scherung beansprucht.

Solche Beanspruchungen treten beispielsweise auf in

• Verbindungselementen wie Nieten, Scherstiften, …
• Verbindungsmittel wie Schweiß-, Klebenaht, …
• Fertigungsverfahren wie Schneiden, Stanzen, …

Der durch die Scherung ausgelöste Spannungszustand ist vergleichsweises komplex.

Wir nutzen entsprechend der üblichen Praxis hier jedoch den Umstand, daß die Schubspannung hinsichtlich der Größenordnung gegenüber anderen Spannungen (Zug, Druck, Biegung) dominiert und treffen zudem die vereinfachende Annahme, daß diese Schubspannung gleichmäßig über den Querschnitt verteilt ist.^{22Daß dem nicht so sein kann, werden wir im nächsten Abschnitt sehen, trotzdem liefert diese Annahme bei der Scherung praxisgerechte Ergebnisse}

Schubspannung durch Scherung

τ = FA

mit

τ = Schubspannung

F= Scherkraft

A= Scherfläche

---

Beispiel:

Aus einem Blech von s=10mm Dicke sollen Ronden des Durchmessers d=42mm gestanzt werden. Die Bruchschubspannung betrage τ_B = 290 Nmm². Welche Preßkraft wird für das Stanzwerkzeug benötigt?

Die abzuscherende Fläche beträgt

Mit der notwendigen Schubspannung

erhalten wir

Schubspannung in der Querschnittsfläche

Bisher haben wir die Schubspannungen im Querschnitt eines Balkens nicht berücksichtigt. Diese müssen jedoch auftreten, um den äußeren Querkräften innerlich das Gleichgewicht zu halten.

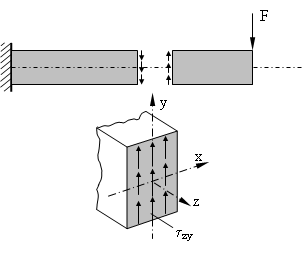
Für die Bezeichnung der Schubspannung gilt folgende Vereinbarung:

• Der erste Index bezeichnet die Koordinate, die normal zur Querschnittsfläche steht.
• Der zweite Index benennt die Richtung, in die die Schubspannung verläuft.
  

Im Gegensatz zur Normalspannung können die Schubspannungen nicht als konstant über der Querschnittsfläche angenommen werden. Die Schubspannungen werden dort, wo sie auf die Querschnittsränder treffen Null.^{23Spannungen können zwar parallel zur Oberfläche eines Körpers verlaufen, jedoch nicht aus diesen austreten.} Ohne Herleitung sei die Gleichung der Schubspannung angegeben.

Schubspannung infolge einer Querkraft

τ_zy = Q_y·S_x(y)b_y (y)I_xx; τ_zx = Q_x·S_y(x)b_x (x)I_yy

mit

Q_x, Q_y = Querkraft in x− oder y−Richtung

S_x, S_y = statisches Moment bezüglich der x− bzw. y−Achse an einer Stelle y(x) des Querschnitts

b_x, b_y = Querschnittsbreite an einer Stelle y(x) des Querschnitts

I_xx, I_yy = axiale Flächenträgheitsmomente

Daraus ergibt sich qualitativ folgender Schubspannungsverlauf über dem Querschnitt.

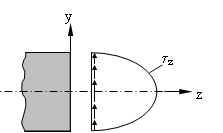
Es ist ersichtlich, daß die größte Schubspannung in der neutralen Faser (Schwerpunkt) auftritt. An den Rändern, wo die Biegespannung maximal wird, ist die Schubspannung Null. Die maximale Schubspannung läßt sich analog zur Scherung bestimmen, indem ein Korrekturfaktor Χ eingeführt wird.

Maximale Schubspannung bei Querkraft

τ_max = Qχ·A

mit

Q = Querkraft

χ = Korrekturfaktor für Schubfläche

A = Querschnittsfläche

Der Korrekturfaktor Χ hängt lediglich von der Form des Querschnitts ab und beträgt beispielsweise

   23 für Rechteckprofil
  χ =
   34 für Kreisprofil

Im allgemeinen wird die Schubspannung gegenüber der Biegespannung vernachlässigt. Erst bei extrem kurzen Balken, wenn die Abmessungen von Balkenhöhe und Balkenlänge gleich werden, erreicht die Schubspannung die Größenordnung der Biegespannung.

Schubspannungen in Balkenlängsrichtung

Im querkraftbelasteten Balken treten korrespondierend zur Schubspannung in der Querschnittsfläche Schubspannungen in achsparallelen Schnitten auf.

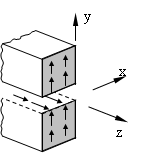
Diese Tatsache läßt sich recht gut veranschaulichen, indem wir zwei lose übereinander liegende Biegebalken unter Belastung im verformten Zustand betrachten.

nicht verbundene Balken, verleimte Balken Während der Biegeverformung werden sich die einzelnen Balken in den Berührungsflächen gegeneinander verschieben. Behindern wir die Balken in diesem Bestreben (durch Nieten, Kleben, Schweißen, …), so werden in diesem Querschnitt Schubspannungen auftreten.

Wie wir in Abschnitt 8 sehen werden, sind diese Schubspannungen nach dem Gesetz der zugeordneten Schubspannungen gleich der Schubspannung im senkrecht zum Längsschnitt liegenden Querschnitt an der jeweiligen Stelle der Schnittführung. Somit tritt in Schwerpunktnähe (neutrale Biegefaser) ebenso die größte Längsschubspannung auf.

Aus diesem Grunde sollte es vermieden werden, Biegebalken in ihrer neutralen Faser zu verbinden oder zu schwächen.

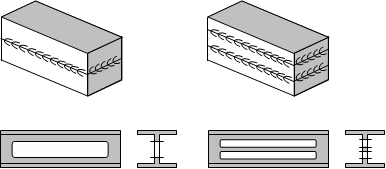
   ungünstig,       besser hinsichtlich Längsschubspannungen

Ein Stab wird mit einem Moment (Kräftepaar) in Richtung seiner Stabachse belastet und so auf Verdrehung beansprucht.

Diese Verdrehungsbeanspruchung wird als Torsion bezeichnet und der Stab als Torsionsstab.

Die mathematische Behandlung von Torsionsstäben beliebigen Querschnitts ist schwierig, da eine Verwölbung des Querschnitts allgemein nicht vernachlässigt werden kann.

Glücklicherweise gilt das nicht für die in der Praxis wichtigen Stäbe mit Kreis- oder Kreisringquerschnitt, die Häufig zur Übertragung von Torsionsmomenten verwendet werden.

Torsionsstäbe mit Kreis(ring)querschnitt

Zur Behandlung der Torsion eines kreisförmigen Stabes treffen wir folgende

Annahmen:

• das Torsionsmoment M_t wirkt parallel zur Stabachse und erzeugt in jedem Stabquerschnitt eine tangential verlaufende Schubspannung τ_t
• die Querschnitte verdrehen sich gegeneinander wie starre Scheiben
• die Verformungen sind klein und es gilt das Hooke´sche Gesetz τ = G · γ

Wir schneiden ein kleines Stück der Länge dz aus dem Torsionsstab heraus und betrachten die um den Winkel dφ gegeneinander verdrehten benachbarten Querschnitte. Wegen der kleinen Verdrehung ist uns nun erlaubt, die Beziehung r·dφ = tanγ·dz der Skizze zu entnehmen. Wir linearisieren mittels tanγ ≈ γ und erhalten unter der Verwendung des Elastizitätsgesetzes

An einem differentiell kleinen Flächenstück dA der Querschnittsfläche

erzeugt die dort wirkende Schubspannung τ_t eine Kraft τ·dA und Moment r·τ·dA um den Kreismittelpunkt.

Die Integration über die gesamte Querschnittsfläche muß das Moment M_t ergeben, also

Unter Verwendung der obigen Beziehung für die Schubspannung τ erhalten wir

Der Verdrehwinkel φ und dessen Ableitung, sowie der Schubmodul ist nicht veränderlich über der Fläche A und wir vereinfachen zu

und erkennen schließlich in

das polare Flächenträgheitsmoment der Querschnittsfläche A.

Wir fassen die Ergebnisse zusammen

Torsion von kreisförmigen Stäben Schubspannung τ_t = M_tI_p·r
Torsionsgleichung G·I_p·φ´= M_t
Kreis I_p = π·d⁴32
Kreisring I_p = π32·(d4a − d4t)

mit

τ_t = Torsionsschubspannung

M_t = Torsionsmoment

I_p = polares Trägheitsmoment

G = Schubmodul

GI_p = Torsionssteifigkeit

φ = Verdrehwinkel

d = Kreisdurchmesser

d_t = Kreisringinnendurchmesser

d_a = Kreisringaußendurchmesser

Als wichtigen Sonderfall betrachten wir zudem einen Stab der Länge Δl mit konstanter Torsionssteifigkeit G·I_p entlang dieser Länge sowie konstantem Torsionsmoment.

Dann erhalten wir aus der Torsionsgleichung

durch beidseitige Integration den

relativen Verdrehwinkel

Δφ = M_tG·I_pΔl