Für die einfachen Grundbeanspruchungen -Zug,/-Druck, -Biegung, -Verdrehung erfolgt der Festigkeitsnachweis durch den Vergleich der rechnerisch ermittelten Spannung mit den bekannten Grenzspannungen für die jeweilige Beanspruchungsart. Diese Grenzspannung wird als maximal mögliche Belastung eines Bauteils angesehen, deren Überschreiten zu einem Versagen des Werkstoffs führt. Ein Bauteilversagen wird irgendwo zwischen

• Trennbruch aufgrund großer Zug-Normalspannungen (sprödes Werkstoffverhalten)
• Gleitbruch (Verformungsbruch) durch die größte Schubspannung (zähes Werkstoffverhalten)
  
  

eingeordnet.

Wir vergegenwertigen uns erneut, daß bei reiner Zugbelastung ja auch Schub und bei reinem Schub (z.B. Torsion) auch Normalspannungen jeweils im 45° -Schnitt zu dieser Belastung auftreten.

Im vorangegangenen Abschnitt haben wir gesehen, das in jedem kleinen Bauteilelement (Rechteck der Größe dxdy) ein überlagerter Spannungszustand aus Normalspannung σ und τ Schubspannung wirkt.

Für eine solche zusammengesetzte, mehrachsige Beanspruchung liegen nun keine entsprechenden Grenzwerte aus Versuchen vor. Es ist insbesondere nicht einfach möglich, aus dem Versagen bei einachsiger Beanspruchung auf das Verhalten bei mehrachsiger Belastung zu schließen.

Aus dieser Verlegenheit heraus wurden bereits in früherer Zeit sog. Bruchhypothesen (Festigkeitshypothesen) aufgestellt, um die Bauteilbelastung anhand einer spezifischen Vergleichsspannung σ_v auf einem einachsigen Spannungszustand zurückzuführen. Von diesen unterschiedlichen Hypothesen haben sich drei als in der Praxis brauchbar erwiesen.

• Hypothese der größten Normalspannung (Hauptspannungshypothese)
• Hypothese der größten Schubspannung (Schubspannungshypothese)
• Hypothese der größten Gestaltänderungstheorie (Gestaltänderungsenergiehypothese)
  
  

Als brauchbar wollen wir eine Hypothese dann ansehen, wenn sie durch entsprechende Versuche weitgehend bestätigt wird.

Hauptspannungshypothese

Dieser Hypothese liegt die Überlegung zugrunde, das die größte Normalspannung bei einem mehrachsigen Spannungszstand (Hauptspannung σ₁) für einen Trennbruch verantwortlich ist, wenn diese den Grenzwert der Trennfestigkeit erreicht.

Gemäß der Gleichung für die Hauptspannung des ebenen Spannungszustands schreiben wir also für die

Vergleichsspannung nach der Hauptspannungshypothese

eignet sich gut für spröde, trennbruchempfindliche Werkstoffe

Mit dieser Vergleichsspannung wird der vorliegende komplizierte Spannungszustand auf den des einfachen Zugstabs reduziert.

Schubspannungshypothese

Diese Hypothese basiert auf der Annahme, daß die größte auftretende Schubspannung für die Zerstörung verantwortlich ist.

Wie dem Mohr´schen Spannungskreis entnommen werden kann, ist

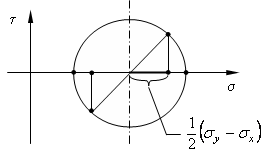
Als Vergleichsspannung wird die Normalspannung im Zugversuch herangezogen. Die Schubspannung, im Schnitt von 45° dazu ist jedoch halb so groß, also

Daraus erhalten wir die

Vergleichsspannung nach der Schubspannungshypothese^{29Diese Hypothese wurde 1864 von H. Tresca aufgestellt. Sie wird häufig nach ihm benannt.}

durch Versuche bestätigt für:

• verformungsfähige Metalle (ausgeprägte Fließgrenze) unter ruhenden Zug-/Druckbeanspruchung
• spröde Werkstoffe unter Druckbelastung

Gestaltänderungshypothese (GE-Hypothese)

Diese Hypothese basiert auf der Annahme, daß derjenige Energieanteil der Materialbeanspruchung, der die Bauteilgestalt ändert, bzw. für den Bruch verantwortlich ist. Unter einem mehrachsigen Spannungszustand erleidet ein Bauteilelement eine Formänderung.

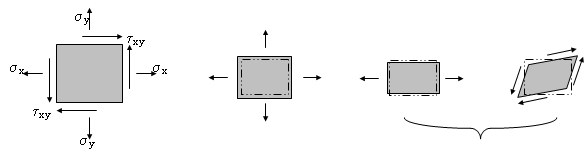
    Formänderung       = Volumenänderung +     Gestaltänderung
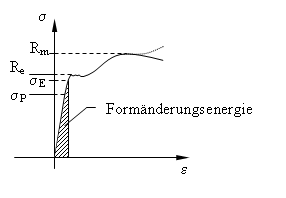
Die Energie oder Arbeit der Verformung des Bauteils entspricht der Fläche unter dem Kurvenverlauf im Spannungs / Dehnungs-Diagramm. Wir verzichten hier auf die

Vergleichsspannung nach der Gestaltänderungsenergiehypothese^{30Diese Hypothese wird auch nach Huber (1872-1950), v. Mises (1883-1953) und Hencky (1851-1951 benannt.}

Besondere Eignung bei:

• dynamischer Bauteilbelastung
• ruhende Beanspruchung zäher Werkstoffe mit nicht ausgeprägter Fließgrenze