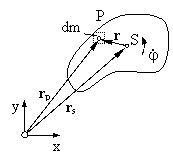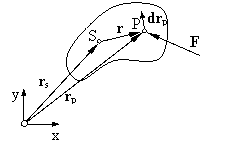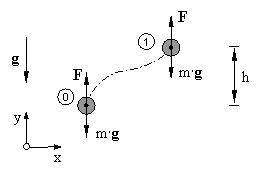
Um die Arbeit näher zu untersuchen, betrachten wir zunächst die Verschiebung der Masse m entlang des differentiellen Verschiebungsvektors dr.

Eine gesonderte Betrachtung des Skalarprodukts

ergibt:

• Die Arbeit ist ein Skalar.
• Die Arbeit ist positiv, wenn Kraft und Verschiebung gleichgerichtet sind.
• Die Arbeit ist negativ, wenn Kraft und Verschiebung entgegengesetzt gerichtet sind.
• Die Arbeit ist null, wenn
  1. die Kraft senkrecht zur Verschiebungsrichtung wirkt
  2. der Kraftangriffspunkt sich nicht bewegt, die Verschiebung also null ist
  3. die Summe aller Kräfte am Angriffspunkt null ist (innere (Gelenk-)Kräfte)
     

Hieraus folgt, daß lediglich die Bahnkomponente der Kraft, also die Projektion des Kraftvektors F auf den Verschiebungsvektor dr Arbeit verrichtet.
Weiterhin besitzen lediglich äußere Kräfte Arbeitsvermögen, Gelenkkräfte dagegen nicht. Die Integration zwischen den Bahnpunkten r₀ und r₁

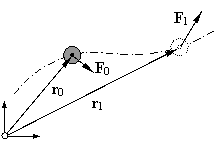
Arbeit als Wegintegral^{9wird auch als Linienintegral bezeichnet} über die Bahnkomponente der Kraft

W = r₁∫r₀F·dr

mit

W = Arbeit

F = Kraft

dr = Verschiebungsrichtung

Die Dimension der Arbeit ist [Kraft%uF0D7Länge] mit der

Einheit der Arbeit

1J = 1Nm mit J=Joule

Damit besitzt die Arbeit dieselbe Dimension wie das Moment. Wohlgemerkt haben wir es jedoch mit unterschiedlichen Effekten zu tun.^{10Das Moment ergibt sich aus dem Kreuzprodukt und die Arbeit aus dem Skalarprodukt von Kraft und Länge.}

Zur Herleitung des Arbeitssatzes ziehen wir das dynamische Grundgesetz in seiner Form für Festkörper heran,

multiplizieren mit dem Verschiebungsvektor dr,

verwenden die Beziehung v = drdt und integrieren entlang des Weges von Anfangspunkt r₀ bis zum Endpunkt r₁ mit den zugehörigen Geschwindigkeiten v₀ und v₁

Der Ausdruck auf der linken Seite der Gleichung entspricht der zu leistenden Arbeit

Auf der rechten Seite ergibt sich nach der Integration die Differenz der kinetischen Energie^{11Bewegungsenergie}.
Damit gilt die

Äquivalenz von Arbeit und Energie:
Energie ist das Vermögen Arbeit zu verrichten.

Gegenüber der Arbeit, die einen Vorgang darstellt, ist die Energie ein Zustand.
Die Dimension der Energie ist analog zur Arbeit [Kraft·Länge] mit der Einheit 1J = 1N.
In allgemeiner Formulierung besagt der

Arbeitssatz der Mechanik:

Die Arbeit, die eine Kraft zwischen zwei Bahnpunkten verrichtet, entspricht der Änderung der kinetischen Energie

W = r₁∫r₀F·dr = 12·mv21 − 12·mv20

Wir bewegen einen Körper im Gravitationsfeld aus der Position 0 in die Position 1.

In vektorieller Komponentenschreibweise ergibt sich

und schließlich nach der Integration

Offensichtlich hat die Bahn keinerlei Einfluß auf die Hubarbeit.

Die Hubarbeit

W_Hub = m·g·h

ist unabhängig von der Bahnform und ergibt sich aus dem Produkt von Gewichtskraft m·g und Höhendifferenz h.

Die Hubarbeit ist äquivalent zur Änderung der potentiellen Energie der Lage eines Körpers im Gravitationsfeld (Potentialfeld).

Die Größe der potentiellen Energie ist offensichtlich von der Wahl des Bezugssystems (Ursprung) abhängig.

Von technischem Interesse ist jedoch grundsätzlich die Potentialdifferenz, die wiederum von der Wahl des Nullniveaus unabhängig ist. Durch das Anheben hat ein Körper potentielle Energie im Sinne eines Arbeitsvermögens gespeichert. Er kann also durch Herabbewegen auf das ursprüngliche Niveau eine -der Hubarbeit entsprechende- Arbeit verrichten.

Wird eine Feder gespannt, so wird eine äußere Kraft benötigt, die mit der Federkraft im Gleichgewicht steht.

Wir betrachten eine Feder mit linearer Kennlinie, d.h.

F = c·(l − l₀)

mit

c = Federkonstante[Nm]

l = gespannte Länge

l₀ = Länge der ungespannten Feder

Verlängern wir nun die Feder von l₀ um l, so benötigen wir einen Kraftverlauf [F = c*l] und müssen dazu die Arbeit

aufbringen. Auch hier wird potentielle Energie gespeichert. Die notwendige Spannarbeit entspricht hierbei ebenso wie die Hubarbeit einer Potentialdifferenz.

Die Federspannarbeit

W_f = 12·c(l21 −l20)

mit

c = Federkonstante

l₁ = Endlänge der Feder

l₀ = Ausgangslänge der Feder

ist äquivalent der Differenz der potentiellen Energie

W_f = E_pf1 − E_pf0

Auch hier ist die Wahl des Nullniveaus beliebig^{12 Meist wird die ungespannte Federlänge als Nullniveau gewählt.}. Die Gleichung gilt sowohl für Zug als auch für Druckfedern.

entgegengerichtet sein. Die erforderliche Kraft wirkt somit in Verschiebungsrichtung. Die Reibungsarbeit ergibt sich also aus

zu

Im Gegensatz zur Hub- und Federspannarbeit ist die Reibungsarbeit vom Weg abhängig. Ebensowenig besitzen Reibungskräfte ein Potential. Die durch Reibungsarbeit erzeugte Reibungsenergie besitzt auch kein mechanisches Arbeitsvermögen^{13Reibungsenergie wird in Wärmeenergie umgesetzt.}, weswegen wir meist auch von Reibungsverlusten sprechen (= dissipative Energie).

Der Energiesatz ist auch unter dem etwas aussagekräftigeren Begriff Energieerhaltungssatz bekannt.

Energieerhaltungssatz

Die Summe aller Energien in einem abgeschlossenen System ist konstant. Dabei kann eine Energie zwar in eine andere Energieform umgewandelt werden, jedoch nicht verlorengehen.

In dieser allgemeinen Form des Energiesatzes werden auch weitere Energieformen als die bisher angesprochenen mit einbezogen, z.B. chemische, elektrische, magnetische, Strahlungs-, Wärme-, Kernenergie.

In der Mechanik betrachten wir ausschließlich die kinetische und potentiele Energie und formulieren den

Energieerhaltungssatz der Mechanik

Die Summe der kinetischen und potentiellen Energie in einem abgeschlossenen mechanischen System ist jederzeit konstant.

E_Kin + E_Pot = const.

Wird einem nicht abgeschlossenen System während eines Vorgangs Energie zugeführt oder abgeführt (z.B. Wärmeenergie), so ist die Differenz der Energie am Ende des Vorgangs gleich dieser zu- oder abgeführten Energie.

Bei Kräften, denen kein Potential zugeordnet werden kann, muß deren Energie über den Arbeitssatz ermittelt werden.

Energiesatz für ein nichtabgeschlossenes System

E_kin1 + E_Pot1 + W_zu + W_ab = E_Kin2 + E_Pot2

mit

E_kin1 = kinetische Energie im Zustand 1

E_Pot1 = potentielle Energie im Zustand 1

W_zu = zugeführte Arbeit (Antrieb)

W_ab = abgeführte Arbeit (Abtrieb, Reibung)

E_kin2 = kinetische Energie im Zustand 2

E_Pot2 = potentielle Energie im Zustand 2

Wir betrachten in Erweiterung des Massenpunkts die ebene Bewegung eines Starrkörpers mit bekanntem Schwerpunkt S.

Die kinetische Energie des Masseteilchens dm in der Umgebung von P ergibt sich analog zur kinetischen Energie der Punktmasse zu

Einsetzen der Geschwindigkeit v_p ergibt

Die Integration über alle Körperpunkte ergibt

Da das statische Moment ∫rdm bezüglich des Schwerpunkts S verschwindet, gilt dies gleichermaßen für ∫r^{^}·dm . Das Integral ∫r²·dm ist definitionsgemäß gleich dem Massenträgheitsmoment J des Körpers.

Damit erhalten wir die

kinetische Energie der ebenen Starrkörperbewegung

E_Kin = 12·mv2s + 12·Jω²

mit

m = Masse des Körpers

J = Massenträgheitsmoment des Körpers

v_s = Geschwindigkeit des Körperschwerpunkts

ω = Winkelgeschwindigkeit des Körpers

Als Leistung^{14P = power (engl.)} P definieren wir die in einem spezifischen Zeitabschnitt verrichtete Arbeit. Wir beziehen also die Arbeit auf die Zeit gemäß

Die Leistung ist damit wie die Arbeit eine skalare Größe und hat die Dimension [Kraft· LängeZeit] mit der Einheit [1W = 1Nms]. Zur näheren Untersuchung der Leistung betrachten wir -wie im vorangegangenen Abschnitt- die ebene Bewegung eines Starrkörpers mit dem Schwerpunkt S. An einem Punkt p des Körpers greift dabei die Kraft F an und verrichtet durch die inkrementelle Verschiebung dr_p des Punkts P die Arbeit dW.

Mit der Leistung als Arbeit bezogen auf die Zeit erhalten wir

Der erste Satz vo1n Euler führt dann auf

Das Skalarprodukt F·r^{^}_sp entspricht dem Moment M der Kraft F und dem Schwerpunkt S.

Damit haben wir die

Leistung zur Bewegung eines Starrkörpers und eines Systems von Starrkörpern^{15Die Erweiterung auf ein Starrkörpersystem ist möglich, wenn die einzelnen Körper mechanisch verbunden sind, d.h. eine Kraft- und Bewegungsübertragung möglich ist.}

P = F·v_A + M·ω

mit

F = Kraft im Körperpunkt A

M = äußeres Moment um Körperpunkt A

v_A = Geschwindigkeit des Körperpunkts A

ω = Winkelgeschwindigkeit des Körpers

Speziell für die reine Drehbewegung gilt als Sonderfall der Leistungsgleichung

Leistung der Drehbewegung um feste Achse

P = M·ω

mit

M = äußeres Moment

ω = Winkelgeschwindigkeit

Wirkungsgrad

Da wir den Leistungsansatz auch für mehrere miteinander mechanisch verbundene Körper verwenden können, müssen wir berücksichtigen, daß in den Gelenken zwischen den Körpern durch Reibungsarbeit Energie abgeführt wird.

Die entsprechende abgeführte Leistung bezeichnen wir als Verlustleistung P_v.

Gemäß der allgemeinen Auffassung vom Wirkungsgrad als

definieren wir den mechanischen Wirkungsgrad η als Verhältnis von Nutzleistung P_N zu zugeführter Leistung P_z.

Die Nutzleistung P_N ergibt sich zudem als Differenz von zugeführter Leistung P_z und Verlustleistung P_v.

Wirkungsgrad eines mechanischen Systems

η = P_NP_z = 1− P_vP_z

mit

P_z = zugeführte Leistung

P_N = Nutzleistung

P_v = Verlustleistung

Für mehrere hintereinandergeschaltete Mechanismen und deren Teilwirkungsgrade gilt

Gesamtwirkungsgrad einer Mechanismenkette als Produkt der Teilwirkungsgrade

η_ges = nΠi=1η_i = η₁·η₂·η₃·...·η_n

mit η_i = Teilwirkungsgrad