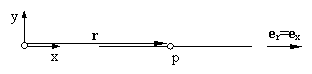Punktbahn

Um die Bewegung eines Punktes zu beschreiben, beziehen wir uns auf ein nicht bewegtes^{1Da es ein absolut ruhendes Bezugssystem nicht gibt, einigen wir uns auf ein nicht beschleunigtes Inertialsystem.} kartesisches Koordinatensystem.

Darin hat der Punkt den Freiheitsgrad f = 2 in der Ebene und f = 3 im Raum.
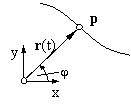
Im Verlauf der Zeit ändert sich die Position p des Punktes und beschreibt so die Bahn r(t).
Unter Verwendung von Polarkoordinaten (r,φ) läßt sich der Ortsvektor des Punktes p formulieren als

Bahn eines Punktes

• r = r·e_r mit
  r = Abstand des Punkts vom Koordinatenursprung
  e_r = Einheitsvektor des Ortsvektors r

Punktgeschwindigkeit

Als Geschwindigkeit des Punktes p ist dessen Lageänderung Δr während des Zeitintervalls Δt definiert.

Im Grenzübergang ist die Geschwindigkeit r^• demnach die zeitliche Ableitung^{2Wir folgen der allgemeinen Konvention und kennzeichnen Ableitungen nach der Zeit mit einem über die betreffende Größe gesetzten Punkt.} des Ortsvektors r eines Punkts p. Die Geschwindigkeit ist ebenfalls ein Vektor.
Um dessen Größe und Richtung näher zu untersuchen, benutzen wir die obige polare Schreibweise des Ortsvektors und erhalten nach der Produktregel

Wir formulieren unter Verwendung des Einheitsvektors e_r die

Geschwindigkeit eines Punktes

• r^• = r^•·e_r + r·φ^•·e_r^{^} mit
  r = Abstand des Punktes vom Koodinatenursprung
  r^• = radiale Abstandsänderungsgeschwindigkeit
  φ^• = Winkelgeschwindigkeit
  e_r = Einheitsvektor des Ortsvektors r

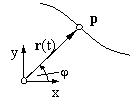Der Geschwindigkeitsvektor r^• wird im zugehörigen Punkt p angetragen und hat die Richtung der Bahntangente in diesem Punkt. Die Geschwindigkeit besteht aus einer radialen Komponente r^•·e_r in Richtung des Ortsvektors r und aus einer zirkularen Komponente r·φ^•·e_r^{^} senkrecht dazu. Die Dimension der Geschwindigkeit ist [Länge/Zeit] mit der gebräuchlichen Einheit [ms] . Im Straßenverkehr wird üblicherweise [kmh = 1000m3600s = 0.278 ms] verwendet.

Punktbeschleunigung

Um zur Beschleunigung zu gelangen, differenzieren wir die Geschwindigkeit erneut.

Mit e_r erhalten wir die

Beschleunigung eines Punktes

r^•• = (r^•• − r·φ^•2)e_r + (r·φ^•• + 2r^•·φ^• )e_r^{^}

mit

r^•• = Radialbeschleunigung

rφ^•2 = Zetripedalbeschleunigung

rφ^• = Zirkularbeschleunigung

2r^•·φ^• = Coriolisbeschleunigung

Die Dimension der Beschleunigung ist [Länge/Zeit²] mit der gebräuchlichen Einheit [ms²] . Da wir im allgemeinen keine recht gute Vorstellung von Beschleunigungen haben, verwenden Autohersteller die Geschwindigkeitsänderung Δv und die benötigte Zeit Δt um die mittlere Beschleunigung a = ΔvΔt zu veranschaulichen, also "beschleunigt von 0 auf 100 km/h in 12s".
Bevor wir auf die allgemeine Punktbewegung näher eingehen, insbesondere die einzelnen Geschwindigkeits- und Beschleunigungskomponenten untersuchen, sollen zunächst zwei wichtige Sonderfälle betrachtet werden:

• geradlinige Punktbewegung
• Kreisbewegung des Punktes

 

Zur Untersuchung der linearen Punktbewegung wollen wir den Koordinatenursprung auf die betreffende Gerade und die x-Achse in Geradenrichtung legen. Unter dieser Voraussetzung vereinfachen sich Beziehungen des vorherigen Abschnitts für Position, Geschwindigkeit und Beschleunigung zu

Die zirkularen Komponenten (alle Glieder mit φ) verschwinden dabei.
Offensichtlich können wir zudem auf den vektoriellen Character verzichten und die kinematischen Funktionen als skalare Beziehungen behandeln. Dabei bevorzugen wir die Bezeichnung Weg s anstelle der x-Koordinate.

Geradlinige Punktbewegung

s=s(t) (Weg)
v = s^•(t) (Geschwindigkeit)
a = s^••(t) = v^•(t) (Beschleunigung)

Wenn bei einer geradlinigen Bewegung ^{3Diese Beziehungen werden auch auf geführte Bewegungen angewandt, deren Verlauf zwar nicht geradlinig ist, wo jedoch lediglich Geschwindigkeit und Beschleunigung in Führungsbahnrichtung interessiert.} der Weg als Funktion der Zeit bekannt ist, lassen sich Geschwindigkeit und Beschleunigung durch einfache, aufeinanderfolgende Differentiation ermitteln. Dummerweise ist bei praktischen Problemstellungen meist eine Aussage über die Beschleunigung gegeben.

Konstante Geschwindigkeit

Unter der Voraussetzung a=0 muß gelten v(t)=v₀.

Eine solche Bewegung mit konstanter Geschwindigkeit heißt gleichförmige Bewegung. Den Weg erhalten wir durch Integration von

mittels Trennung der Variablen

und Definition der Anfangswerte s₀, t₀ die Integrationskonstante

gleichförmige Bewegung eines Punktes

s = s₀ + v₀·(t − t₀)

v = v₀

a = 0

Konstante Beschleunigung

Für die gleichmäßig beschleunigte Bewegung gilt a(t)=a₀. Wir beginnen die Zeitmessung zum Zeitpunkt t₀. Zu dieser Zeit besitzt unser Punkt die Anfangsgeschwindigkeit v(t=t₀)=v₀ und einen Anfangsweg von s(t=t₀)=s₀.
Durch Integration von

erhalten wir nach einer Trennung der Variablen

mit

gilt für die Geschwindigkeit

Nochmalige Integration von

ergibt

und liefert für t = t0 den Anfangswert

und damit den Weg zur Zeit t

gleichmäßig beschleunigte Bewegung eines Punktes

s(t) = v₀(t − t₀)+12·a₀(t − t₀)²

v(t) = v₀+a₀(t − t₀)

a(t) = a₀

Gleichförmige Beschleunigungen spielen in der Natur (freier Fall) und der Technik (Antriebe) eine bedeutende Rolle.

 Die Punktbewegung auf einer Kreisbahn ist ein praktisch bedeutsamer Sonderfall der allgemeinen Bewegung des Punktes.

Zur Bewegungsbeschreibung legen wir zulässigerweise den Ursprung des Bezugskoordinatensystems in den Kreismittelpunkt. Dadurch bleibt der Betrag von r während der Kreisbewegung konstant. Aus den Beziehungen für Geschwindigkeit und Beschleunigung der allgemeinen Punktbewegung verschwinden daher alle Komponenten mit r^• und r^•• . Speziell bei der Kreisbewegung hat sich zudem die Bezeichnung ω für die Winkelgeschwindigkeit φ^• durchgesetzt.

Kreisbewegung des Punktes

r = r·e_r (Position)

r^• = r·ω·e_r^{^} (Geschwindigkeit)

r^•• = − r·ω²·e_r + r·α·e_r^{^} (Beschleunigung)

mit

r·ω = Umfangsgeschwindigkeit

r·ω² = Normalbeschleunigung

r·α = Umfangsbeschleunigung (Zirkularbeschleunigung)

Ein Punkt p auf dem Kreisumfang hat eine Geschwindigkeit vom Betrag r·ω, die in Richtung der Kreistangente in p verläuft (r^{^}). Bei einer Änderung der Winkelgeschwindigkeit ω erfährt der Punkt p eine Umfangsbeschleunigung r·ω^• ebenfalls in tangentialer Richtung. In jedem Fall wirkt auf den Punkt p eine Normalbeschleunigung r·ω² , die zum Kreismittelpunkt hin gerichtet ist^{4Zentripetalbeschleunigung, korrespondierend zur entgegengerichteten Zentrifugalkraft, die den Punkt vom Mittelpunkt wegzieht.}.

Die Winkelgeschwindigkeit wird üblicherweise in der Einheit s⁻¹ angegeben. Dies ist implizit als rads zu lesen und bedeutet, daß bei ω = 1s⁻¹ ein Winkel von 1rad = 180°/{π} ≈ 57 pro Sekunde überstrichen wird.
In der Praxis wird häufig die Drehzahl n zur Bemessung der Winkelgeschwindigkeit verwendet und legt - im allgemeinen - die "Anzahl Umdrehungen pro Minute [Umin] " fest. Es gilt hierbei der

Zusammenhang zwischen Winkelgeschwindigkeit und Drehzahl^{5Beachte: Es ist hier keine Umrechnung von min in s enthalten.}

ω = 2π·n

mit

ω = Winkelgeschwindigkeit

n = Drehzahl

Bei konstanter Winkelgeschwindigkeit läßt sich der zurückgelegte Winkel durch die Differenzen ermitteln

Winkel bei konstanter Winkelgeschwindigkeit

φ(t) = phi₀ + ω·(t − t₀)

Häufig interessiert uns ausschließlich die tangentiale Bewegung eines Punktes auf der Kreisbahn.
Der Weg, den der Punkt auf dem Kreisumfang zurücklegt, gehorcht der bekannten Beziehung

mit dem zurückgelegten Winkel φ in [rad].
Durch Differentiation erhalten wir die skalaren kinematischen Gleichungen der

Umfangsbewegung des Punktes auf dem Kreis

s = r·φ

v = r·ω

a = r·α

In der Technik (z.B. bei Transportvorgängen) haben wir es oft mit zusammengesetzten einfachen Bewegungen zu tun. Diese gehorchen häufig abschnittsweise den in den vorangegangenen Kapiteln beschriebenen Gesetzmäßigkeiten.
Zur Veranschaulichung stellen wir die Bewegungsabläufe in sogenannten Bewegungsdiagrammen dar.
Gebräuchlich sind hierbei Diagramme über

• der Zeit, s(t); v(t); a(t)-Diagramme
• dem Weg, v(s); a(s)-Diagramme

Bevor wir anhand eines Beispiels die Vorgehensweise näher beleuchten, wollen wir eine Berechnungstabelle für die kinematischen Größen t, s, v und a aufstellen. Dabei beschränken wir uns auf den speziellen, aber praktisch bedeutsamen Sonderfall a=const.
Zunächst formulieren wir die Bewegungsgleichungen der gleichmäßig beschleunigten Bewegung in der Differnzenschreibweise.
Mit

schreiben wir die

gleichmäßig beschleunigte Bewegung in Differenzenschreibweise

Δs = v₀·Δt + 12·aΔt²

Δv = a·Δt

Δa = 0

Für 4 Differenzen stehen insgesamt 2 Gleichungen zur Verfügung (die dritte ist recht nutzlos). Damit lassen sich mit zwei gegebenen Größen aus

die restlichen beiden ermitteln.
So erhalten wir beispielsweise Δv und a aus gegebenen Δs und Δt mittels

Δt	Δs	Δv	a= const.
2)	2)	2(ΔsΔt − v0)	2(ΔsΔt2 − v0Δt)
2)	(v0 + 12·Δv)Δt	2)	ΔvΔt
2)	v0·Δt + 12·aΔt2	a·Δt	2)
Δsv0 +12·Δv	2)	2)	(v0 + 12·Δv)ΔvΔs
− v0 + √(v0 + 2aΔs)a(Δsv0 für a = 0)	2)	− v0 + √(v20 + 2aΔs)	2)
Δva1)	(v0 + 12·Δv)Δva1)	2)	2)

1) nicht gültig für a = Δv = 0 2) gegebene Größen v0 als Anfangsbedingung oder vom vorhergehenden Bewegungsabschnitt bekannt.

Von den vier kinematischen Größen Δt, Δs, Δv, a genügen 2, um die beiden restlichen zu ermitteln.
Für die Bewegungsabschnitte in einem kinematischen Diagramm sind damit zunächst die Übergangswerte zu bestimmen. Die Anfangswerte sind grundsätzlich vorzugeben.

Ausgehend von bekannten Anfangswerten

können wir sukzessive die Übergangswerte

mittels der bekannten Differenzen des Bewegungsabschnitts i mittels

ermitteln, da wir für Weg und Geschwindigkeit grundsätzlich stetige Funktionen über der Zeit erhalten (die Zeit selbst ist ohnehin monoton steigend). Die Beschleunigung ist dagegen konstant während eines Beschleunigungsabschnitts und ändert sich dazwischen sprunghaft.
Die Bewegungsgrößen innerhalb eines Abschnitts ergeben sich dann aus

Die Vorgehensweise sei an einem Beispiel näher erläutert.