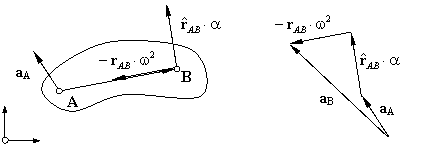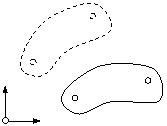
Nachdem wir nachgewiesen haben, daß die allgemeine ebene Bewegung eines Körpers als überlagerte Translation und Rotation aufgefaßt werden kann, wollen wir nun zeigen, daß der momentane Geschwindigkeitszustand des Körpers als reine Drehbewegung um einen ganz bestimmten Punkt -den Momentanpol- zu interpretieren ist.

Als einzigen Anhaltspunkt auf der Suche nach dem Momentanpol haben wir seine Eigenschaft, momentan geschwindigkeitslos zu sein. Es muß also gelten

Wir lösen die Gleichung nach dem gesuchten Richtungsvektor von Punkt A zum Pol auf

und wenden den Drehoperator auf die Gleichung an und erhalten den

Momentanpol der ebenen Bewegung

r_APol = v^{^}_Aω

Geometrisch finden wir -entsprechend der Interpretation der Momentangleichung- den Momentanpol auf der Geraden durch einen Punkt A senkrecht zu dessen Geschwindigkeitsvektor v_A.

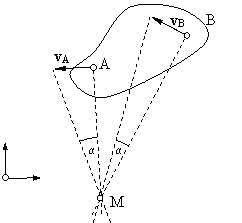
Sind die Bewegungsrichtungen (Geschwindigkeitsvektoren) zweier Punkte eines Körpers gegeben, so erhalten wir den Momentanpol als Schnittpunkt der Geraden durch diese Punkte jeweils senkrecht zu deren Bewegungsrichtungen.

Die Dreiecke zwischen Körperpunkt, Momentanpol und Endpunkt des zugehörigen Geschwindigkeitsvektors sind für beliebige Körperpunkte ähnlich. Den Winkel α erhalten wir aus

Position

Zur näheren Untersuchung der Starrkörperbewegung beziehen wir die Lage eines Körpers auf ein festes Bezugskoordinatensystem und markieren zwei Körperpunkte A und B.

Die Lage des Punkts B können wir über dessen Ortsvektor r_B im Bezugssystem beschreiben. Dieser ergibt sich aus der Vektorsumme

Unter Verwendung des Winkels φ zwischen r_AB und der positiven x-Achse können wir auch

schreiben. In der vorstehenden Gleichung hängen alle Größen von der Zeit ab, bis auf r_AB -dem Abstand der Körperpunkte A und B- der sich ja entsprechend unserer Starrkörperdefinition nicht ändern darf.

Geschwindigkeit

Die Geschwindigkeit des Punktes B erhalten wir analog zur Punktbewegung durch formale Differentiation nach der Zeit t.

Mit v statt r^• und ω anstelle von φ^• schreiben wir

Die Körperbewegung bzw. dessen Geschwindigkeit läßt sich in eine reine Translation (Schiebung) und eine Rotation (Drehung) zerlegen.

1. Satz von Euler^{6Leonhard Euler (1707-1783)} für die Geschwindigkeit

v_B = v_A + r_AB^{^}·ω

mit

v_B = Geschwindigkeit des Punktes B

v_A = Geschwindigkeit des Punktes A

r_AB^{^}·ω = Tangentialgeschwindigkeit der Drehung von B um A

Beschleunigung

Analog zur Geschwindigkeit erhalten wir die Beschleunigung durch die Ableitung der Geschwindigkeit nach der Zeit.

Wir verwenden a, ω, α für r^••, φ^• und φ^•• erhalten die

Beschleunigung eines Punktes B eines Körpers (1. Satz von Euler für die Beschleunigungen)

a_B = a_A + r_AB^{^}·ω²

mit

a_B = Beschleunigung des Punktes B

a_A = Beschleunigung des Punktes A

r_AB^{^}·α = Tangentialbeschleunigung der Drehung von B um A

− r_AB·ω² = Normalbeschleunigung der Drehung von B um A